2.5 부분공간의 기저와 차원

---

이 글은 Edwith로 부터 제공되는 주재걸 교수님의 "인공지능을 위한 선형대수" 강의를 듣고 요약하였으며, 개인 공부를 위해 부족한 부분을 위해 필요한 개념들을 추가하여 작성하였습니다.

---

 

이번 절(2.5)에서는 부분공간의 기저와 차원 정의 및 개념을 알아보고, 예제를 직접 풀어면서 이해를 돕고자 한다.

 

• Linear independence (2.4)

• span (2.5)

• subspace (2.5)

 

Span and Subspace (Subspace of ℝ)

---

Subspace & Span 

다음 아래에 세 가지 조건을 만족하면 ℝ(n) 차원의 subspace H 라고 불린다. 

 

[그림 1] Subspace of ℝ's Definition

 

Example 1. 

v1과 v2 벡터의 Span은 Linear combination을 한 것이다.

 

[그림 2] Example 1

Example 2. 

2차원 공간에 있는 직선 L 은  u 와 v 로 이루어진 subspace인가?

 

[그림 3] Example 2

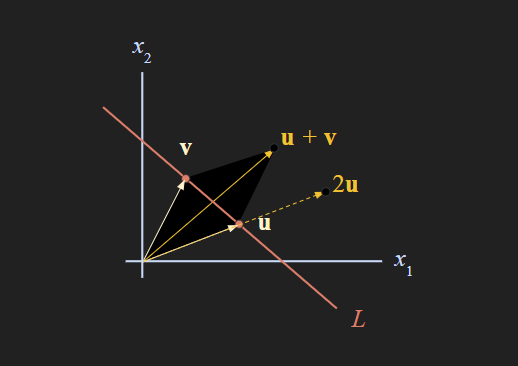
subspace의 조건 3가지를 모두 만족하지 않기 때문에 subspace가 아니다.

 

 

 

Basis of a Subspace

---

 지금까지 Subspace 및 Span에 대해 알아봤지만, Subspace를 구성하는 Vector들 간에 서로 독립인 경우 Basis of a subspace 라고 한다. 

 

• Fully spans the given subsapce H 
• Linearly independent (i.e, no redundancy)

 

[그림 4] 기하학적 표현

[그림 5] Basis for a Subspace's Definition

 

 

Non-Uniqueness of Basis

---

평면을 구성하고 있는 Basis는 유일한가? 

 

[그림 6] Non-Uniqueness of Basis

 

방향은 같지만 크기(scalar multiple)가 다른 셋으로도 충분히 표현가능하기 때문에 그렇지 않다. (Change of Basis)

 

하지만, 기저를 구성하는 벡터의 수(Dimension of Subspace)는 유일하다. 

 

 

Dimension of Subspace

---

• Basis는 Unique하지 않았다면, 무엇이 Unique한 성질을 가질까?
• H에 대해 다른 basis가 존재하더라고 벡터의 수는 고유한 값을 가진다.
• Dimension of H 라고 부르며, dim H 라고 표기, 차원이라고 읽는다.

 

예를 들어 보자. 

[그림 7] The dimension of H ; 2

[그림 7]의 subspace of H 에 대한 dimension(차원)은 2 이다. 

 

 

Standard Basis for ℝ

---

앞서 Basis는 unique하지 않았던 이유가 크기가 다양했기 때문이다. 벡터의 크기를 모두 1로 고정한 것을 Standard Basis라고 한다. 

 

[그림 8] Standard Basis

 

standard basis로 변경된 벡터의 기호는 보통 e로 표기함.

 

 

Column Space of Matrix

---

 

[그림 8] Column Space of Matrix

 

 

Matrix with Linearly Dependent Columns

---

[그림 9] Matrix with Linearly Dependent Columns

 

Rank of Matrix

---

[그림 10] Rank of Matrix's Definition

 

 

Summary

---