이 글은 Edwith로 부터 재공되는 주재걸 교수님의 "인공지능을 위한 성형대수" 강의를 듣고 요약하였으며, 개인 공부를 위해 부족한 부분을 위해 필요한 개념들을 추가하여 작성하였습니다.
이번 절(2.4)에서는 선형 독립과 선형 종속 정의 및 개념을 알아보고, 예제를 직접 풀어면서 이해를 돕고자 한다.
-
Linear independence (2.4)
-
span (2.5)
-
subspace (2.5)
Recall: Linear System
우선 본론으로 들어가기 전에 앞 절에서 다룬 "Linear System"을 다시 한번 상기 시켜보자.

[그림 1]처럼 데이터가 주어졌을 때, 선형 시스템을 Matrix equation과 Vector equation 으로 표현할 수 있다.
Uniqueness of Solution for A x = b
해가 존재하기 위해서는 반드시 b ∈ Span{a1, a2, a3} 의 조건을 만족해야한다.
(Span에 대한 개념은 다음 절에서 설명할 예정)

해가 존재하는 경우에도 "무수히 많은 해"와 "유일한 해"가 존재하는 경우가 있다. 그렇다면, 유일한 해가 존재하려면 어떤 조건일까? 또는 유일한 해가 존재하려면 어떤 조건일까? 라는 것을 Linear System 관점에서 선형 독립과 종속을 이용하여 관계를 아래와 같이 정리할 수 있다.
Theorem 2. Existence and Uniqueness Theorem


Linear Independence
선형 독립 정의 (Formal)

선형 독립 정의 (Practical)

Linear Independence of Matrix Columns

참고 : "if and only if"는 필요충분조건
Example 1. Matrix의 Column들을 가지고 선형 독립인지 판단해보자.

선형 독립의 정의를 이용하면 Homogeneous Linear System을 만족시키기 위해 필요한 해는 오직 모두 0인 trivial solution 밖에 없다. 따라서, 선형 독립이다.
선형 종속 정의
선형 독립의 정의를 명확히 알면 선형 종속의 정의도 쉽게 이해할 수 있다.

Eaxmple 2. Matrix의 Column들을 가지고 선형 종속인지 판단해보자.

free variable이 존재하는 경우 가능한 solution이 매우 많아지고, 선형 종속임을 알 수 있다.
Two Definitions are Equivalent
선형 독립의 Formal 및 Practical 한 두 정의는 같은 의미이다.
만약, Matrix를 구성하는 Vector들이 서로 선형 종속이며, nontrivial solution을 가진다고 하자.
그때의 조건을 가지고 아래와 같이 정리하면 선형 종속 셋에 대한 특성을 알 수 있다.
Characterization of Linearly Dependent Sets

Geometric Understanding of Linear Dependence
Characterization of Linearly Dependent Sets을 기하학적으로 해석해보자.

Linear Dependence I
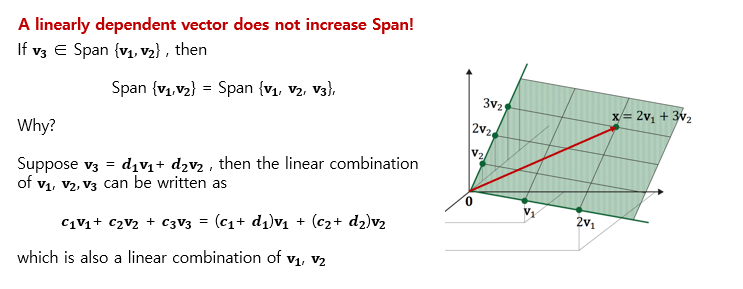
Linear Dependence II

Eaxmple 3. Matrix의 Column들을 가지고 선형 종속인지 판단해보자.

Linear Dependence III

Eaxmple 4.
이번 절에서 배운 개념을 이용하여 아래 Matrix의 Column들을 가지고 선형 종속 또는 독립을 판단해보자.

Sets of One Vector

0이 아닌 Vector가 단 하나만 존재할 때, 그 Vector는 선형 독립이다.
Sets of two vectors

두 개의 vector로 이루어진 vector set이 서로 종속이면 하나의 vector는 다른 하나의 vector에 상수배로 표현할 수 있다.
두 개의 vector로 이루어진 voctor set이 서로 독립이면 하나의 vector는 다른 하나의 vector에 상수배로 표현할 수 없다.
Summary
-
linearly dependent / independent
-
linear dependency of matrix columns
-
sets of one vector / two vectors
-
Theorem 7-9
'Linear Algebra (선형대수학) > Ch 2. 선형시스템 및 선형변환' 카테고리의 다른 글
| 2.2 Solution Sets of Linear Systems (0) | 2020.03.25 |
|---|---|
| 2.8 전사함수와 일대일함수 (0) | 2019.11.19 |
| 2.6 선형변환 (0) | 2019.11.19 |
| 2.5 부분공간의 기저와 차원 (0) | 2019.11.19 |
| 2.1 선형방정식과 선형시스템 (0) | 2019.11.19 |




댓글