이 글은 Edwith로 부터 제공되는 주재걸 교수님의 "인공지능을 위한 선형대수" 강의를 듣고 요약하였으며, 개인 공부를 위해 부족한 부분을 위해 필요한 개념들을 추가하여 작성하였습니다.
이번 절(2.6)에서는 선형 변환 정의 및 개념을 알아보고, 예제를 직접 풀어면서 이해를 돕고자 한다.
Transformation
Transformation (function, mapping) 의 정의는 다음과 같다.

vector x (n 공간)를 어떤 규칙에 의해서 Linear Tranformation을 했을때 vector T (x) (m 공간)로 변환하는 과정이다.
[용어 정리]
-
Domain : Set of all the possible values of x (정의역)
-
Co-domain : Set of all the possible values of T(x) (공역)
-
Image : a mapped output y, given x
-
Range : Set of all the output values mapped by each x in the domain (치역)

Example 1 : Matrix Multiplication (or Linear Transformation)
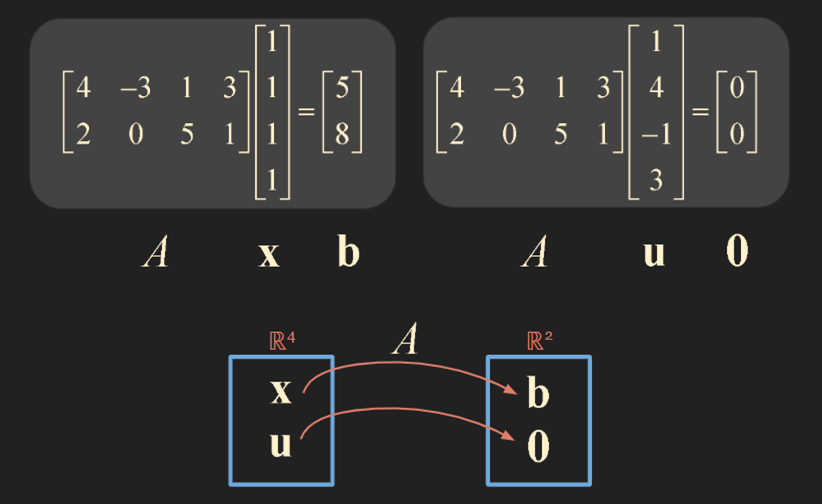
4차원 내 x 벡터를 matrix A 에 의해 선형 변환하면 2차원 내 b 벡터로 변환된다.
4차원 내 u 벡터를 matrix A 에 의해 선형 변환하면 2차원 내 0 벡터로 변환된다.
Example 2 :
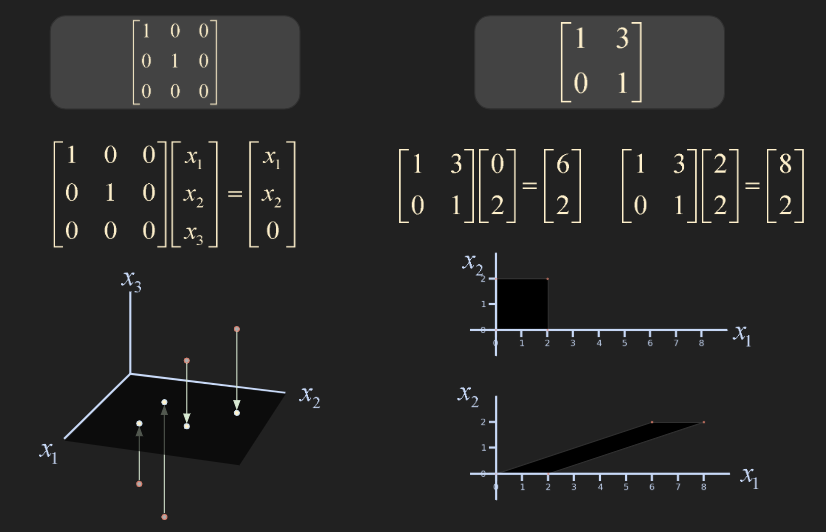
- 3차원 내 벡터를 2차원 평면 공간으로 변환시키는 예제 (좌)
- 2차원 공간 내 벡터를 선형 변환하여 2차원 다른 공간으로 변환시키는 예제를 Shear Transformation 라고 함(우)
Linear Transformation

Example 3

The Matrix of Linear Transformation
어떤 Matrix Transformation을 찾을때, 어떤 특정 Vector를 Transformation해서 나온 Image만 알고 있으면 Matrix Transformation을 알 수 있다. 예제로 풀어보면 다음과 같다.

위 에서 구한 Matrix Transformation은 unique(유일)하고, 이를 standard matrix for the linear transformation T 라고 한다. 증명은 생략
참고 : https://colah.github.io/posts/2014-03-NN-Manifolds-Topology/
Neural Networks, Manifolds, and Topology -- colah's blog
Neural Networks, Manifolds, and Topology Posted on April 6, 2014 topology, neural networks, deep learning, manifold hypothesis Recently, there’s been a great deal of excitement and interest in deep neural networks because they’ve achieved
colah.github.io
Summary
-
transformation
- linear transformation
-
Matrix transformation
- Matrix of Linear Transformation
'Linear Algebra (선형대수학) > Ch 2. 선형시스템 및 선형변환' 카테고리의 다른 글
| 2.2 Solution Sets of Linear Systems (0) | 2020.03.25 |
|---|---|
| 2.8 전사함수와 일대일함수 (0) | 2019.11.19 |
| 2.5 부분공간의 기저와 차원 (0) | 2019.11.19 |
| 2.4 선형독립과 선형종속 (0) | 2019.11.19 |
| 2.1 선형방정식과 선형시스템 (0) | 2019.11.19 |




댓글