본문 바로가기
CS231

Lecture 7 : Training Neural Networks II

by Keep It Simple, Stupid! 2020. 4. 16.

Part 2

  • Fancier optimization
  • Regularization
  • Transfer Learning

 이번 장에서 다룰 내용은 위와 같으며 최적화를 다루기 전 아래 내용을 확인하고 들어가자.

GD (batch gradient descent) : 한 번의 업데이트를 위해 모든 데이터 계산

  • 손실함수는 $J = \sum_{i=1}^{N}{error}$이며, $\sum_{i=1}^{N}$가 모든 데이터를 의미한다.
  • 단점 : 한 번의 업데이트를 위해 모든 데이터가 계산에 포함되므로 속도가 느림
  • 특징 : loss function이 convex한 경우 global mimimum을 보장하고, nonconvex인 경우 local minimum을 보장

SGD (stochastic gradient descent) : 한 번의 파라미터 업데이트를 위해 하나의 훈련데이터 계산

  • 파라미터를 업데이트하는 식은 아래와 같다.

$$\theta_{t+1} = \theta_t - \eta\nabla_{\theta}J(\theta ; x^{(i)},y^{(i)})$$

  • 장점 : GD보다 훨씬 빠르게 업데이트 진행
  • 단점 : 매 업데이트마다 데이터 하나에 의해 결정되다보니, 들쑥날쑥한 크기의 gradient로 파라미터를 업데이트
  • 특징 : 분산이 큰 gradient(들쑥날쑥한 gradient)는 SGD가 local minimum에 빠져나오게 만들 수도 있지만 반대로 수렴을 방해할 수 있음

Mini-batch GD (mini-batch gradient descent) : 임의의 batch-size로 구성된 손실함수를 이용해 파라미터 업데이트

  • $J = \sum_{i=1}^{N}{error}$이며, $\sum_{i=1}^{N}$가 모든 데이터가 아닌 mini-batch로 뽑힌 데이터를 의미한다
  • 장점 : GD보다 훨씬 빠르게 업데이트, gradient도 크기가 상대적으로 들쭉날쭉하지 않다.(분산이 적음)
  • 단점 : 분산이 적기 때문에 local minimum에 빠질수도 있다.?

Optimization

 위 그림은 간단하게 2개의 paramet(W_1, W_2)으로 부터 Loss를 시각화한 그림이며, 최종 목적은 Loss가  가장 낮은 부분(붉은색)에서의 W_1과 W_2를 찾는 것이다. 이를 Vanillan Gradient Descent(SGD)라 부르며, SGD는 여러 Problem(단점)이 존재한다. 

Problem with SGD (1)

 등고선 간격이 좁으면 경사가 높고, 등고선 간격이 넓으면 경사가 완만하다라는 것은 누구나 아는 내용이다. SGD를 진행하면 경사가 완만한 방향으로는 아주 느리게, 경사가 높은 방향으로는 신호의 차이가 크게(jitter) 업데이트되는 것이다. 특히, loss function이 고차원인 경우 Hessian matrix의 최대값과 최소값의 비율이 큰데, 이런 원인이 문제점을 발생하게 되는 것 같다.

Problem with SGD (2)

ⓐ와 같이 loss function의 gradient가 0일때, 운이 없으면 update를 종료하는 local minima에 빠져 나오지 못하게 된다. (global mimima를 찾아야함)

ⓑ와 같이 loss function의 gradient가 0일때, 운이 없으면 saddle point에 빠져 나오지 못하게 된다. (saddle point : parameter 1개(x축) 기준, gradient가 0인 점에서의 "-" 및 "+" 방향에서의 gradient가 서로 다른 부호를 가지는 점) 

참고 : loss function이 고차원일수록 saddple points가 많다고 함

Problem with SGD (3)

 minibatch의 random sample로 부터 얻어지는 gradient는 loss의 noise가 있기 때문에 goal에 도달하기 전 헤매다가 (시간을 소비) 도달한다. 즉, batch라면 noise가 없을텐데, minibatch인 경우 전체를 대변하지 못하기 때문에 noise가 생길 수 밖에 없음

학생의 질문 : GD를 이용하면 위의 문제점들을 해결할 수 있을까요?
답변 : GD는 단지 SGD보다 속도 측면에서 단점이 크기 때문에 사용하지 않는것이다. 

 

Solution 1 : SGD + Momenum

  IDEA : 시간에 따라 velocity(vx)를 유지하는 것이다. 그리고 우리의 gradient(dx) 추정치를 velocity(속도)에 더하는 것이다. (즉, 기울기 방향으로 힘을 받아 물체가 가속된다는 물리 법칙과 같다.) 

 위는 강의자료 PDF를 참고한건데, learnig_rate부분과 code 부분이 다름, 컨셉만 확인하고 아래식을 참고!

$$v_t = \gamma v_{t-1} + \eta \nabla_{\theta_t}J(\theta_t)$$

$$\theta_{t+1} = \theta_t - v_t$$

  • $\gamma$ 는 마찰 계수이며, 주로 0.9 또는 0.99로 설정하여 사용(기존 속도를 강제로 줄이게 함)

 

 SGD에서 존재하던 Gradient대신 velocity를 더한 값이기 때문에 기존 SGD의 문제점들을 극복 할 수 있게된다. (e.g. gradient가 0이 나왔지만, 기존 velocity가 있었기 때문에 0이 아닌 업데이트하여 local minima에 빠지거나, saddle point에 빠져도 goal을 향해(탐험) 다가갈 수 있음)

  • local minima 해결
  • saddle point 해결
  • zig-zag (gradient noise) 문제점 해결 : 파랑색 noise가 덜하다! 이유는?

속도는 parameter지만 초기화를 0으로 설정해도 성능에는 무관하다.

 다음 아래 왼쪽 그림은 위에서 설명한 Momentum update이며.  momentum의 단점은 속도를 못줄이고 원치 않는 업데이트를 게속하게 된다. 따라서 이런 문제를 해결하기 위해 나온 알고리즘이 Nesterov Momentum이며 오른쪽 그림을 살펴보자. 

Solution 2 : NAG (Nesterov Accelerated Gradient)

 Nesterov 모멘텀의 핵심 아이디어는 다음과 같다. 만약 현재 파라미터 벡터가 x라는 어떤 위치에 있다고 치고 위의 모멘텀 엄데이트를 보자. 만일 위의 integrate velocity 과정에서 뒷항없이 v = mu * v 만 있다고 가정하면, 다음 위치로 x + mu * v가 “예견”될 것이다. 그러므로 이전의/오래된 위치 x 대신 예견된 위치 x + mu * v에서 그라디언트를 계산하는 것이 합리적일 수 있다.

 Nesterov 모멘텀. 지금 위치(붉은색 원)에서 모멘텀에 의해 연두색 화살표의 끝점으로 이동할 상황이다. Nesterov 모멘텀은 현재 위치에서 그라디언트를 계산하는 것이 아니라 이 "예견된" 위치(화살표 끝점)에서 그라디언트를 계산한다.

 NAG는 일반 Momentum보다 평균적으로 더 좋은 성능을 보인다. 일반 Momentum 방식은 기울기에 따라 이동을 한 후 속도에 따라 다시 이동하는 방식이지만, NAG는 속도에 따라 미리 이동한 후 기울기를 고려하여 속도를 변화시키기 때문에, Momentum의 속도를 이용한 빠른 이동이라는 이점을 살리면서 더욱 안정적인 이동을 할 수 있게 된다.

Solution 3 : AdaGrad

 지금까지 논의된 접근법들(Momentum, NAG)은 모든 파라미터에 똑같은 학습 속도를 적용하였다. 학습 속도의 튜닝(tuning)은 계산이 많은(expensive) 작업인지라, 데이터에 맞추어(adaptively) 자동으로 학습 속도를 정하는 방법을 찾고자 많은 사람들이 노력하였다. 파라미터별로 학습 속도를 다르게 하고 이를 데이터-맞춤으로 정하려는 노력들 또한 있었다. 이러한 방법들은 보통 또다른 초모수(hyperparameter) 세팅이 필요하긴 하지만, 이 초모수는 넓은 범위에서 잘 작동하는 편이라 일반적인 학습 속도 튜닝보다는 덜 까다롭다. 이번 절에서는 실전에서 마주칠 수도 있는 주요 데이터-맞춤 방법들을 조망해본다.

Adagrad는 데이터-맞춤 학습속도 조정 방법 중 하나이고 Duchi et al. 에서 처음 제안되었다.

 
# Assume the gradient dx and parameter vector x
cache += dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

 위에서 변수 cache는 그라디언트 벡터의 사이즈와 동일한 사이즈를 갖고 있다. cache의 각 성분은 (해당 성분에 대응하는) 그라디언트의 제곱값들을 계속 추적하고 있고, 파라미터 업데이트에서, 성분별로, 일종의 표준화 기능을 수행한다. 주목할 점은, 높은 그라디언트값을 갖는 웨이트값(weight)들은 점점 실질적인 학습속도(effective learning rate)가 감소하고 / 그라디언트 값이 낮거나 업데이트가 거의 없는 웨이트값들은 실질 학습속도가 증가한다는 것이다. 놀랍게도 제곱근(square root) 연산이 여기서 중요한 비중을 차지한다. 제곱근이 없다면 알고리즘의 성능이 많이 나빠진다. 변수 eps는 분모가 너무 0에 가깝지 않도록 안정화 역할을 하고 주로 1e-4에서 1e-8의 값이 할당된다. Adagrad의 단점이 있다면, 딥러닝의 경우에는, 학습 속도가 단조적이라 너무 한 방향으로 급진적(aggressive)으로 나가거나, 혹은 학습을 너무 빨리 멈출 가능성도 있다.

Q1 : Adagrad는 어떻게 업데이트 되는가?

A1 : Momentum에서 사용하던 velocity 대신 gradient squared term을 사용한다. gradient를 계속 활용

 분모가 grad_squared인데, 이는 처음부터 지금까지의 기울기를 누적한 값이다. 때문에, 높은 그라디언트값을 갖는 웨이트값(weight)들은 점점 실질적인 학습속도(effective learning rate)가 감소하고 / 그라디언트 값이 낮거나 업데이트가 거의 없는 웨이트값들은 실질 학습속도가 증가한다는 것이다. (위에서 설명)

Q2 : 오랜 시간 동안 스텝 크기는 어떻게됩니까?

A2 : step에 따라 grad_squared가 커지기 마련이다. 이는 분모가 커지면 0으로 가기 때문에, 학습을 멈추게 되는 문제점이 있다.

위의 문제점을 해결하기 위해 RMSProp가 나오게 된다. 

Solution 4 : RMSProp

 RMSProp 업데이트는 Adagrad를 간단히 조정하여 급진적이고 단조감소하는 학습속도를 경감시켰다. 어떻게? 제곱 그라디언트의 평균(Adagrad처럼)이 아니라, 이동평균(moving average)을 사용한다. 

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

 여기서 decay_rate는 초모수이고 보통 [0.9, 0.99, 0.999] 중 하나의 값을 취한다. 주목할 점은 += 업데이트는 Adagrad와 동등하지만, cache가 지나치게 커지는 것을 막아준다. 따라서 RMSProp은 여전히 각 가중치값을 (그것의 과거 그라디언트) 값으로) 조정하여 성분별로 실질 학습속도를 비슷하게 만드는 효과는 갖고 있지만, Adagrad처럼 학습 속도가 단조적으로 줄지는 않는다.

 

지금까지 했던 최적화 기법을 두 가지 성질로 구분할 수 있다.

  • Momentum 계열 : Momentum, NAG
  • Ada 계열 : Adagrad, RMSProp

이제 서로의 장점을 결합한 방법이 Adam이다.

Solution 5 : Adam

Adam은 그나마 최근에 제안된 방법인데 RMSProp에 모멘텀(momentum)을 혼합한 것처럼 보인다. 간단하게 쓰면 업데이트는 다음과 같다:

m = beta1*m + (1-beta1)*dx
v = beta2*v + (1-beta2)*(dx**2)
x += - learning_rate * m / (np.sqrt(v) + eps)

Q1 : 첫번째 timestep에서 무슨일이 발생하는가?

A1 : first_moment, second_moment가 0이고, beta1 = 0.9, beta2 = 0.999로 설정해주기 때문에 second_moment는 0에 가깝다. 분모가 작아지면 update값이 매우 증가하기 때문에, 값이 이상한 방향으로 튈 수 있는 문제점이 있다.

 위의 문제점을 해결하고자 Bias correction을 code에 추가함으로써 업데이트시 분모가 0으로가는것을 막아주는 역할을 해준다. 

 Adam의 효과가 가장 좋으며, 실제 모델링에서도 Adam을 많이 사용한다.

추가 참고문헌:

 Unit Tests for Stochastic Optimization는 (지금까지 제안된) 확률적 최적화(stochastic optimization) 방법들을 평가하는 표준적인 테스트들을 제안하고 있다.

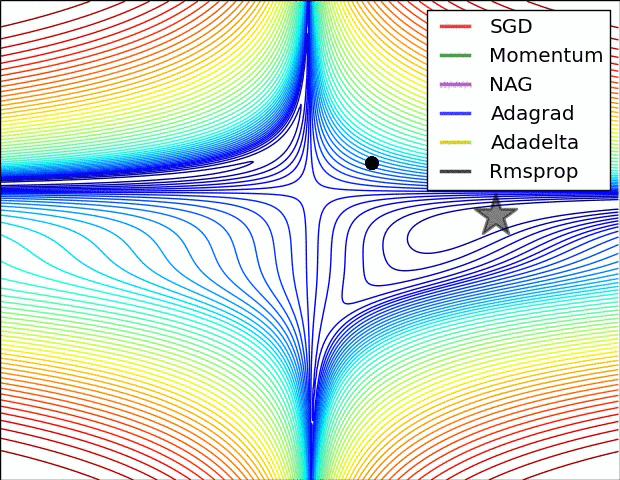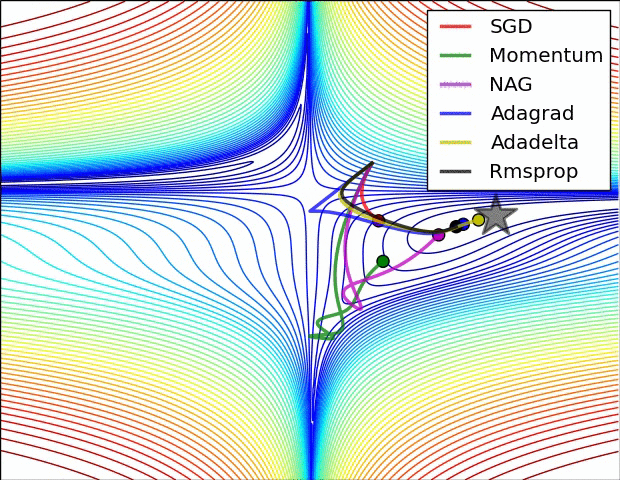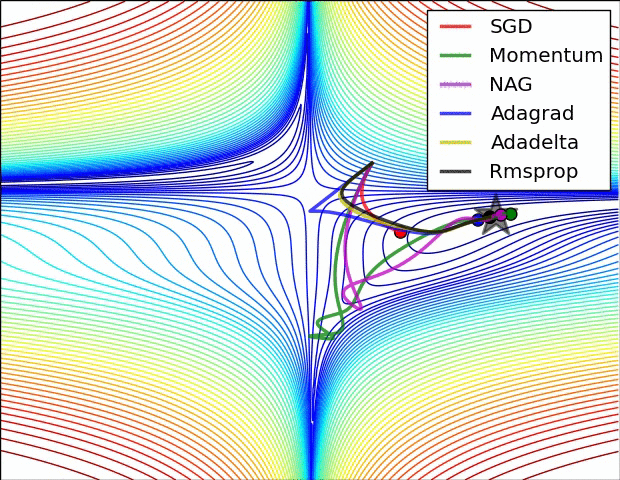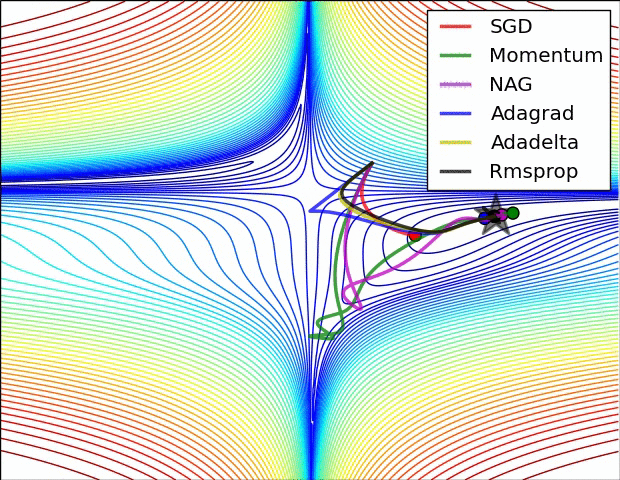
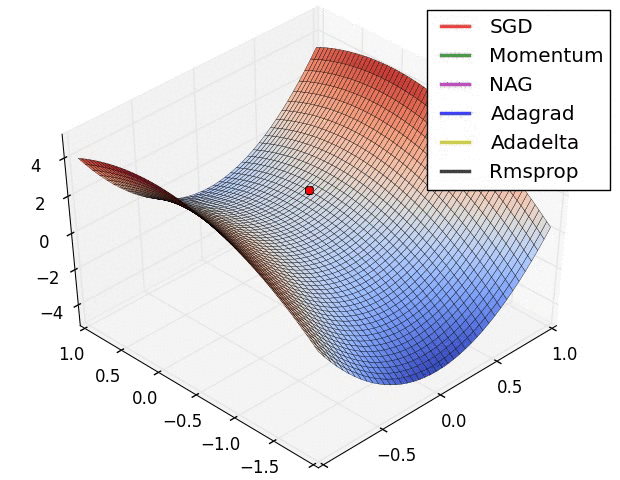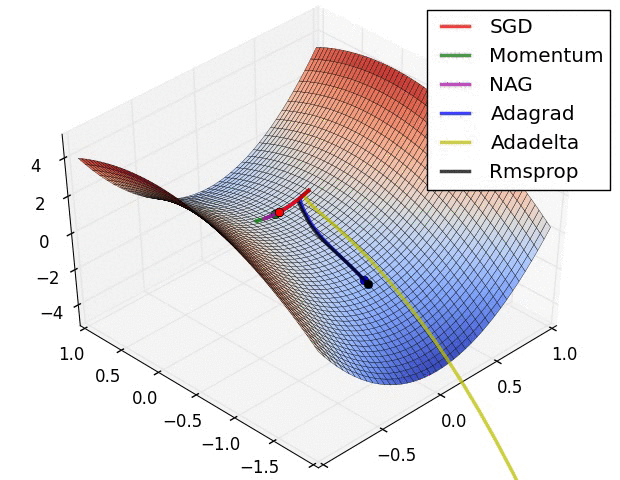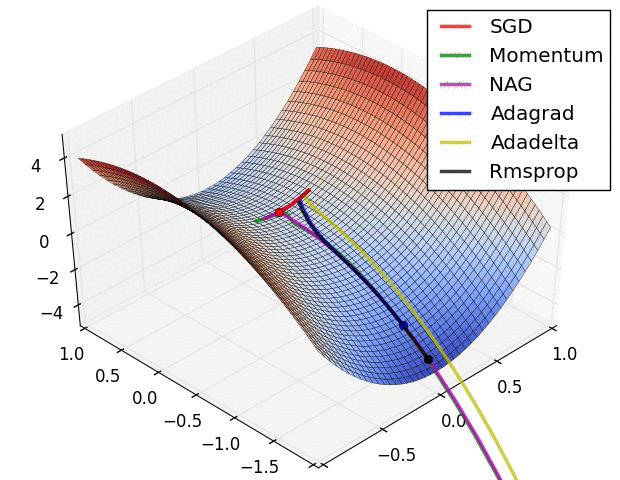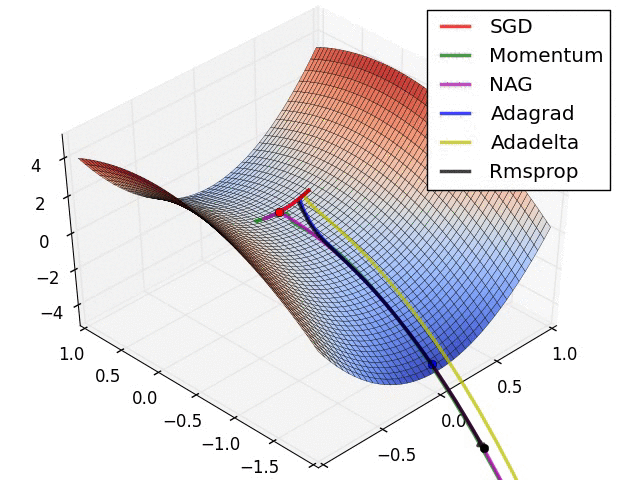
 위 동영상이 학습 과정에서의 동역학(dynamics)를 직관적으로 이해하는데 도움이 되길 바란다. 왼쪽: 손실 함수의 등고선 위에서 각 최적화 알고리즘들의 시간(iteration)에 따른 변화. 모멘텀-기반 방법론들의 "급가속" 행동들을 주목하라. 이게 최적화를 마치 언덕을 내려가는 공처럼 보이게 만든다. 오른쪽: 목적함수에 안장점(saddle point)가 있을 때의 시각화. 안장점은 그라디언트가 0이지만 헤시안 행렬의 고유치(eigenvalue)에 양수/음수가 섞여있을 때 발생한다. SGD는 안장점에서 빠져나오는 데 매우 힘든 시간을 겪는다. 반대로, RMSprop같은 알고리즘들은 안장의 방향으로 매우 작은 그라디언트를 마주하게 되지만 분모-표준화 성질 덕분에 이 방향의 실질 학습속도를 높아질 수 있고 따라서 이 방향으로 빠져나올 수 있다. Images credit: Alec Radford.

학습 속도 담금질 (Annealing the learning rate)

 지금까지 다룬 최적화 기법들은 모두 learning_rate라는 hyperparamter를 가지고 있다. 

 깊은 신경망의 훈련에서 시간에 따라 훈련 속도를 담금질(anneal, 조정)하는 건 언제나 도움이 된다. 이 직관을 기억해 두면 도움이 된다: 높은 학습 속도에서는, 전체 시스템이 너무 높은 운동 에너지를 갖고 있어서 파라미터 벡터가 혼돈스럽게 튀고, (손실 함수의) 좁고 깊숙한 골짜기 안으로 쏙 들어가서 정착하기 힘들다.
그러면 학습 속도를 언제 줄일 것인가? 좀 tricky할 것이다. 우선 천천히 줄여봐라. 그러면 오랜 시간동안 거의 제자리에서 혼돈스럽게 왔다갔다 할 것이다. 그렇지만 너무 빨리 줄이면 전체 시스템이 너무 빨리 식을 것이고, 갈 수 있는 최적의 장소에 도달하지 못할 수 있다. 학습속도를 감소시키는 방법은 보통 다음 세 가지가 있다.

 
  • 계단식 감소 (step decay) : 몇 에폭마다 일정량만큼 학습 속도를 줄인다. 전형적으로는 5 에폭마다 반으로 줄이거나 20 에폭마다 1/10씩 줄이기도 한다. 이 숫자들은 전적으로 문제와 모형의 타입에 의존한다. 실전에서는, 우선 고정된 학습 속도로 검증오차(validation error)를 살펴보다가, 검증오차가 개선되지 않을 때마다 학습 속도를 감소시키는 (이를테면 0.5정도?) 방법을 택하기도 한다. 
  • 지수적 감소 (exponential decay) : 위 두번째 식이다. 여기서 t는 반복 횟수이다 (물론 에폭을 단위로 해도 된다.) 나머지들은 hyperparamter이다.
  • 1/t decay : $\alpha = \alpha_0 / (1 + k t )$  꼴을 뜻하고 여기서 $a_0, k$는 초모수이고 $t$는 반복 횟수이다.

실전에서는 계단식 감소 방식이 조금 더 선호될만 한데, 관련된 초모수들(몇 에폭마다 감소시킬지, 그리고 감소율)이 kk에 비해서 해석이 더 쉽기 때문이다. 마지막으로, 계산 자원이 충분하다면, 감소율을 좀 더 낮춰서 오랜 시간동안 (모형을) 훈련시켜라.

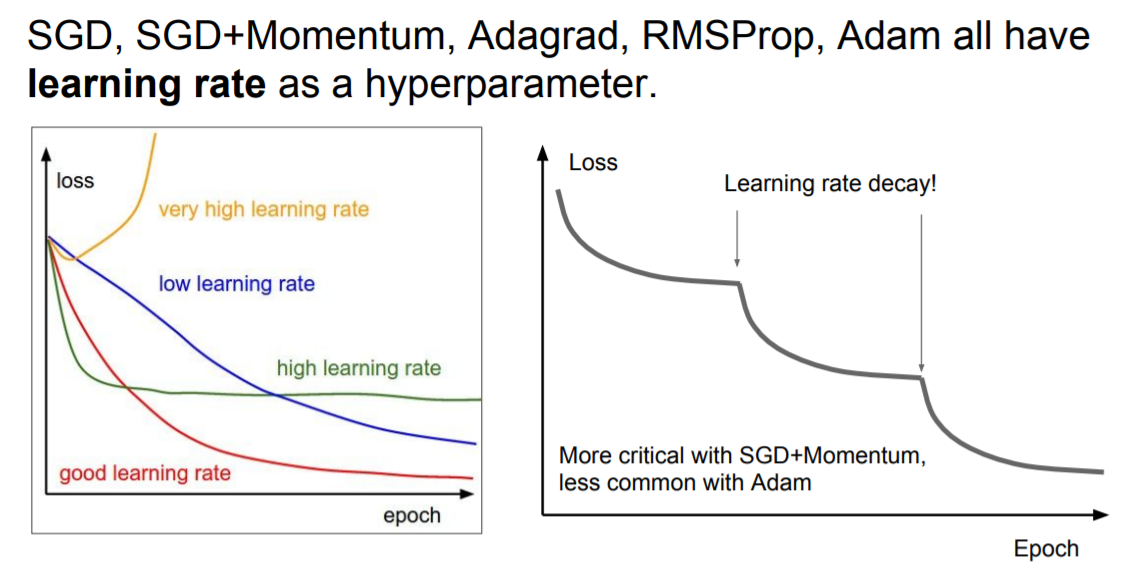 위에서 사용한 방식은 Resnet에서 활용한 step learning rate decay 이다. 이는 Adam보다 SGD+Momentum에서 더 잘먹힌다고 합니다.

First-Order Optimization

 지금까지 gradient를 구할때 1차 미분을 이용하여 optimization을 했다. 하지만, 2차 미분을 활용하여 gradient를 갱신할 수 있다.

Second-Order Optimization

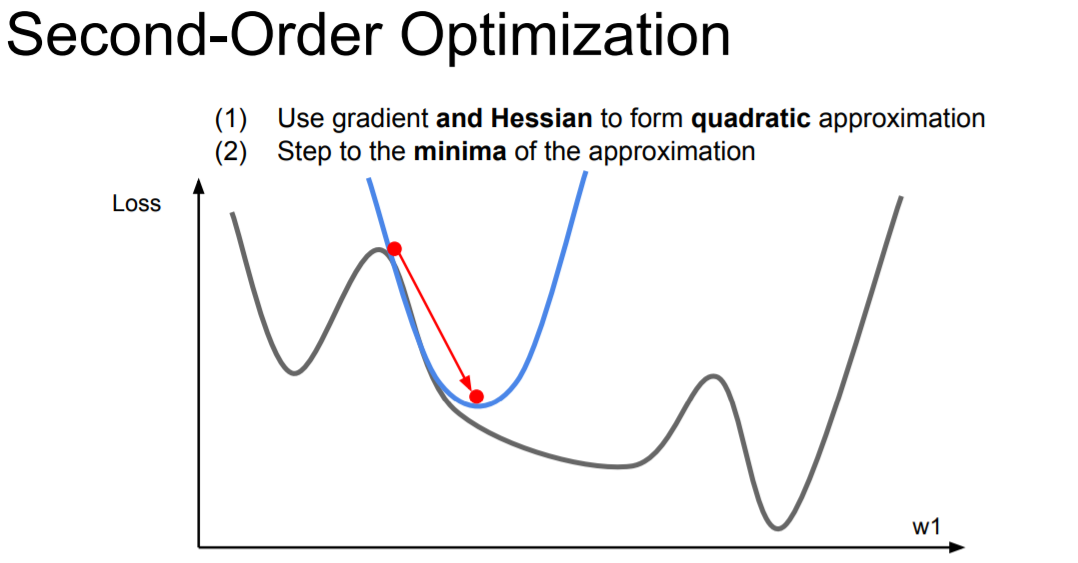 딥러닝의 맥락에서 두 번째로 대중적인 최적화 방법은 뉴턴 방법(Newton’s method)인데 다음과 같은 업데이트 방식을 뜻한다.

$$x \leftarrow x - ([H f(x)])^{-1} \nabla f(x)$$

 여기서 $Hf(x)$는 헤시안 행렬(Hessian matrix)로, (다변수 함수의) 2차 미분으로 이루어진 정방행렬을 뜻한다. $\nabla f(x)$항은 (그라디언트 감소 Gradient Descent에서 보았던) 그라디언트 벡터이다. 직관적으로 헤시안 행렬은 어떤 함수의 국지적인 곡률(curvature)을 뜻하고 이 정보로 더 효율적인 업데이트를 수행할 수 있다. 특별히, 헤시안 행렬의 역행렬을 곱함으로써, 휨이 약한 방향으로는 더 공격적으로 그리고 휨이 강한 방향으로는 짧게짧게 움직일 수 있다. 일차 근사 방법에 비해 뉴턴 방법이 가지는 강점은, 위의 업데이트 공식을 보면 학습 속도(learning rate)에 대한 초모수(hyperparameter)가 없다는 것이다.

 그렇지만 위의 업데이트는 거의 모든 실제 상황에서는 쓸모가 없는 게, 공식 그대로(explicitly) 헤시안 행렬을 계산한다면 (역행렬을 취하는 일 포함하여) 상상도 못할 시간과 메모리가 필요하다. 예를 들면, 모수가 백만개 정도인 신경망은 [1,000,000 x 1,000,000] 크기의 헤시안 행렬을 필요로 하고 이는 3725GB의 램(RAM)을 필요로 한다. 그 결과로 다양한 유사-뉴턴 방법이 역-헤시안 행렬을 근사하기 위해 고안되었다. 이 방법론들 중 L-BFGS가 가장 대중적이다. L-BFGS는 시간(iteration)에 따른 그라디언트의 변화를 (간접적으로) 근사에 이용한다. 즉, 전체 행렬은 절대 계산되지 않는다.

 그렇다고 해도, 메모리 걱정을 없앴다고 할지라도, L-BFGS를 그냥 적용하자면 큰 단점이 하나 있는데 바로 전체 훈련 집합(traning set) 전체를 대상으로 계산하여야 한다는 점이다. 수백만 개체가 있는 그 데이터셋 말이다. 배치(Batch)-SGD와는 달리, 미니배치(mini-batch)에서 L-BFGS가 작동하게 하는 방법은 좀더 꼼수를 필요로 하며 활발한 연구 분야이다.

Q1 : What is nice about this update?

A1 : Hyperparamter(learning rate)가 없어서 편리함

Q2 : Why is this bad for deep learning?

A2 : Hessian has $O(N^2)$ elements Inverting takes $O(N^3)$ N = (Tens or Hundreds of) Millions

위의 문제점을 해결하고자 나온게 BGFS이다.

Beyond Training Error

Model Ensembles

1. Train multiple independent models

2. At test time average their results

Enjoy 2% extra performance

 실전에서, 신경망(neural network)의 성능을 몇 퍼센트 끌어올릴 수 있는 믿을 만한 방법이 하나 있는데 바로 여러 개의 독립적인 모형을 만들고 테스트 때 그들의 평균 예측을 취하는 것이다. 앙상블에 관여하는 모형이 많아지면, 보통 성능은 단조적으로 개선된다 (비록 개선 정도가 점점 떨어질지라도). 게다가, 앙상블 내에서 모형의 다양함이 늘어날수록 성능의 개선은 더 극적이다. 아래는 앙상블을 구축하는 몇 가지 방법이다.

  • 같은 모형, 다른 초기화 (Same model, different initializations). 교차 검증으로 최고의 초모수를 결정한 다음에, 같은 초모수를 이용하되 초기값을 임의로 다양하게 여러 모형을 훈련한다. 이 접근법의 위험은, 모형의 다양성이 오직 다양한 초기값에서만 온다는 것이다.
  • 교차 검증 동안 발견되는 최고의 모형들 (Top models discovered during cross-validation). 교차 검증으로 최고의 초모수(들)를 결정한 다음에, 몇 개의 최고 모형을 선정하여 (예. 10개) 이들로 앙상블을 구축한다. 이 방법은 앙상블 내의 다양성을 증대시키나, 준-최적 모형을 포함할 수도 있는 위험이 있다. 실전에서는 이를 수행하는 게 (위보다) 쉬운 편인데, 교차 검증 뒤에 추가적인 모형의 재훈련이 필요없기 때문이다.
  • 한 모형에서 다른 체크포인트들을 (Different checkpoints of a single model). 만약 훈련이 매우 값비싸면, 어떤 사람들은 단일한 네트워크의 체크포인트들을 (이를테면 매 에폭 후) 앙상블하여 제한적인 성공을 거둔 바 있음을 기억해 두라. 명백하게 이 방법은 다양성이 떨어지지만, 실전에서는 합리적으로 잘 작동할 수 있다. 이 방법은 매우 간편하고 저렴하다는 것이 장점이다.
  • 훈련 동안의 모수값들에 평균을 취하기 (Running average of parameters during training). 훈련 동안 (시간에 따른) 웨이트 값들의 지수 하강 합(exponentially decaying sum)을 저장하는 제 2의 네트워크를 만들면 언제나 몇 퍼센트의 이득을 값싸게 취할 수 있다. 이 방식으로 당신은 최근 몇 iteration 동안의 네트워크에 평균을 취한다고 생각할 수도 있다. 마지막 몇 스텝 동안의 웨이트값들을 이렇게 “안정화” 시킴으로써 당신은 언제나 더 나은 검증 오차를 얻을 수 있다. 거친 직관으로 생각하자면, 목적함수는 볼(bowl)-모양이고 당신의 네트워크는 극값(mode) 주변을 맴돌 것이므로, 평균을 취하면 극값에 더 가까운 어딘가에 다다를 기회가 더 많아질 것이다.

 모형 앙상블의 단점이 하나 있다면 테스트 샘플에 모형을 적용할 때 평가(evaluation)에 더 시간이 걸린다는 점이다. 흥미로운 독자는 Geoff Hinton의 “Dark Knowledge”에서 영감을 얻을 수도 있겠다. 여기서의 아이디어는 좋은 앙상블 모형을 하나의 모형으로 “증류”하는 것인데, 앙상블 모형의 로그-가능도(log-likelihood)를 어떤 변형된 목적함수로 통합하는 작업과 관련이 있다.

 

 빨강 부분은 loss function의 값이 작은 곳을 의미하는데, 이 부분에서 learning rate를 강제적으로 높여 탐험함으로써 다른 다른 지역에 수렴할 수 있도록 하는 것이다.

 위 방법은 자주 사용하지 않기 때문에 Pass!

 참고 : 기계학습에서는 앙상블 학습을 애용한다. 앙상블 학습은 개별적으로 학습시킨여러 모델의 출력을 평균을 내어 추론하는 방식이다. 신경망의 맥락에서 얘기하면, 가령 같은 (비슷한) 구조의 네트워크를 5개 준비하여 따로따로 학습시키고, 시험 때는 그 5개의 출력을 평균 내어 답하는 것이다. 앙상블 학습을 하면 신경망의 정확도가 몇%정도 개선된다는  것이 실험적으로 알려져 있다. 앙상블 학습은 다음에 배울 드랍아웃과 밀접하다. 드롭아웃이 학습 때 뉴런을 무작위로 삭제하는 행위를 매번 다른 모델을 학습시키는 것으로 해석할 수 있기 때문이다. 그리고 추론 때는 뉴런의 출력에 삭제한 비율(e.g. 0.5)을 곱함으로써 앙상블 학습에서 여러 모델의 평균을 내는 것과 같은 효과를 얻는 것이다. 즉, 드롭아웃은 앙상블 학습과 같은 효과를 대략 하나의 네트워크로 구혀현했다고 생각할 수 있다.

Regularization

 위에서는 여러 모델을 가지고 성능(Test set의 정확도)을 향상시키기 위해 앙상블 기법을 소개했었다. 하지만 "하나의 모델을 가지고 성능을 향상시키는 방법은 무엇일까?" 라는 질문에 답하면, 앞 장에서 오버피팅을 억제하는 방식으로 손실 함수에 가중치의 L1 및 L2 Norm을 더한 weight deacy(가중치 감쇠)방법으로 regularization을 소개했었다.

 weight decay는 간단하게 구현할 수 있고 어느 정도 지나친 학습을 억제 시킬 수 있었다. 그러나 신경망 모델이 복잡해지면 가중치 감소만으로는 대응하기 어려워진다. 이럴 때 필요한 기법이 Dropout(드롭아웃)이라는 기법을 이용한다.

 드롭아웃은 뉴런을 임의로 삭제하면서 학습하는 방법이며, 훈련 때 은익층의 뉴런을 무작위로 골라 삭제한다. 삭제된 뉴런은 위의 오른쪽 그림과 같이 신호를 전달하지 않게 된다.

 훈련 때는 데이터를 흘릴 때마다 삭제할 뉴런을 무작위로 선택하게 된다. 훈련 시에는 순전파 때마다 mask에 삭제할 뉴런은 False로 표시하는 것이다. mask는 H1(or H2)와 형상이 같은 배열을 무작위로 생성하고, 그 값이 p(dropout_ratio, 0.5) 보다 큰 원소만 True로 설정하게 된다. 역전파 때의 동작은 ReLU와 같다. 즉 순전파때 신호를 통과시키는 뉴런은 역전파 때도 신호를 그대로 통과시키고, 순전파 때 통과시키지 않은 뉴런은 역전파 때도 신호를 차단하게 된다.

 하지만, 시험 때는 반드시 각 뉴런의 출력에 훈련 때 삭제한 비율을 곱하여 출력을 해야하는 이유를 직관적으로 위에서 보여주고 있다.

 predict 함수을 보면 dropout을 적용하지 않았지만 히든 레이어 출력 데이터에 p 만큼 스케일링 한 것을 주목할 필요가 있다. 테스트 과정에서 모든 뉴런은 모든 입력 데이터를 받기 때문에 학습 과정에서 얻을 수 있는 출력값과 동일한 조건으로 맞추어 보정해야한다. dropout 확률 p=0.5 인 경우를 가정해 보자. 테스트 과정 동안 뉴런의 출력 값은 모두 1/2만큼 줄어들어야 하는데 이는 학습 과정 동안 뉴런 출력 데이터의 기대값과 동일하게 맞추기 위함이다. 뉴런 x가 있을때 dropout 적용하지 않은 출력 데이터가 있다고 가정하자. dropout을 적용하면 이 뉴런에서의 기대값은 px+(1−p)0가 되는데 이는 1−p의 확률로 뉴런의 출력 데이터 값이 0이 되기 때문이다. 테스트 과정에서는 모든 뉴런을 사용하기 때문에 동일한 기대값을 갖기 위해서는 x→px로 보정해 주어야 한다. 또 다른 관점에서 보면 p만큼 값을 줄이는 과정은 모든 가능한 dropout 마스크를 적용한 후 그 결과를 이용하여 ensemble prediction을 수행하는 것으로 해석 할 수 있다.

 위에서 소개한 방법은 테스트 과정에서 뉴런 출력에 p를 곱하는 연산이 수행해야 하는데 이는 원하지 않는 방식인 경우가 많다. 테스트 과정에서의 성능은 매우 중요한 이슈이기 때문에 많은 경우에 inverted droptou 방식이 더 선호된다. 이는 스케일링 연산을 학습 과정에서 적용하고 테스트 과정에서는 추가적인 스케일링 연산없이 바로 사용하는 방식이다. 이 기법의 또 다른 장점은 만약 dropout을 수정하기로 했을때 prediction 코드에는 여전히 변화가 없다는 것이다. Inverted dropout은 다음과 같이 구현할 수 있다.

 dropout이 처음 소개된 이후로 실제 적용 사례에서 나타난 성능 향상의 근본 원인과 기존의 다른 regularization 기법과의 관계등에 대한 수많은 연구가 진행되었다. 관련하여 다음의 자료들을 읽어보는 것인 도움이 될 것이라 생각된다.

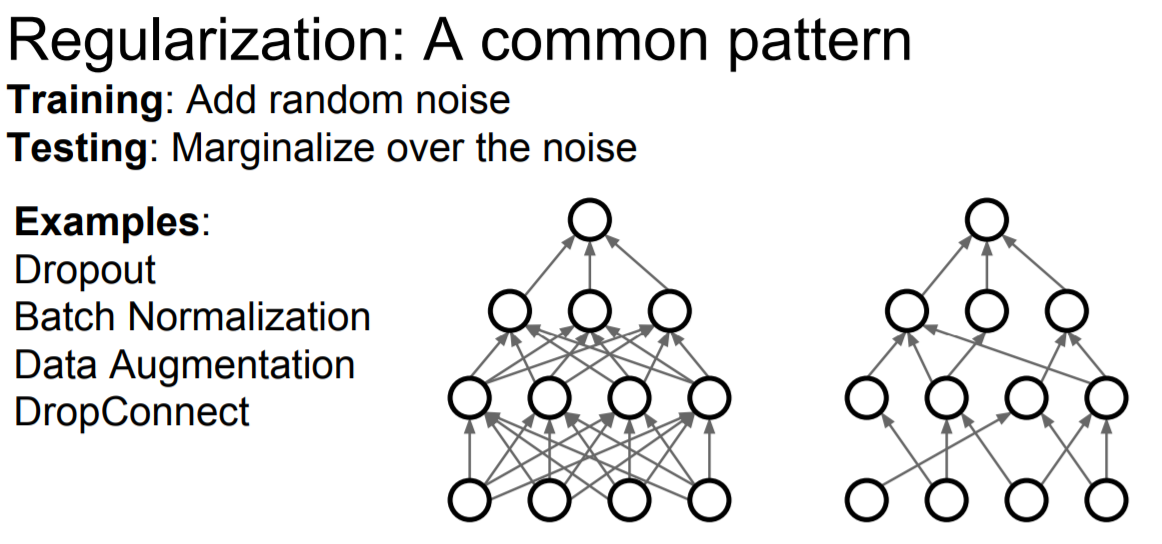
 dropout은 일반적인 전략을 구체화시킨 하나의 예시라고 한다. 학습할 때는 무작위성을 추가하 train data에 너무 fit하지 않게 하는 것이다. 그리고 테스트 때는 무작위성을 평균화시켜 사용하는 것이다. 

Data Augmentaion

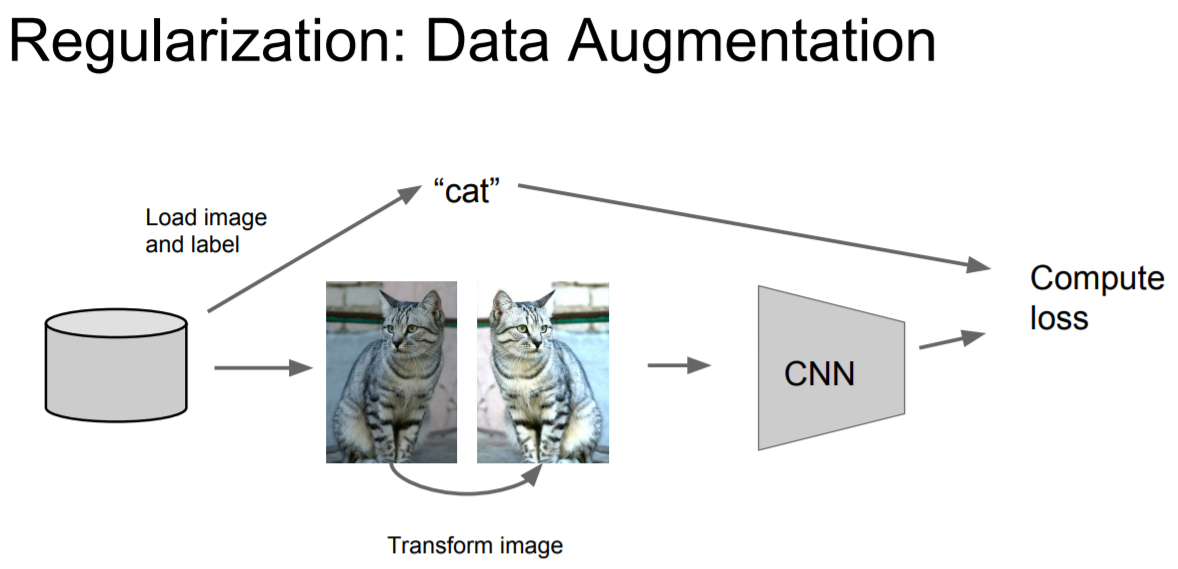 정규화의 또 다른 기법은 data augmentation이다. image에서의 data augmentation는 다양한 방법이 존재한다. 고양이 그림은 "Horizontal Flips(tranform)"시켜도 여전히 고양이다. 

Random crops and scales

Train : 이미지를 임의의 다양한 size로 crop(잘라서) 학습에 사용할 수 있다. 그래도 일부는 고양이의 이미지를 가지고 학습. (예시, 코너에 붙어 있는 224 이미지 4장 + 가운데 있는 224 이미지 1장으로 총 5장)

Test

  • 위에서 얻어진 데이터셋을 5개의 scale로 resize 한다.
  • 위에서 얻어진 size별로 다시, 224 x 224 의 crop 진행 하는데, 5(4 corners + 1center) x 2(flip) = 10개의 성능을 비교

Randomize contrast and brightness


Transfer learning

“You need a lot of a data if you want to train/use CNNs” 에 대한 편견을 깨버리는 아이디어

 1. Train on Imagenet : 우선 Imagenet과 같은 아주 큰 데이터셋으로 학습을 시킨다.

 2. 새롭게 추가할 c개의 Class를 가진 Small Dataset인 경우, 위에서 미리 훈련된 모델을 가지고 우리가 가진 작은 데이터셋에 적용시키는 것이다. 단지 FC-C부분만 Train할때 초기화 시키고 나머지 부분은 그대로 사용하는 것이다. 즉, 마지막 layer만 가지고 데이터를 학습시키는 것이다. 

 3. 만약 새롭게 추가할 data가 더 많다면, FC-C 부터 FC-4096 2개의 layer까지 초기화 시키고 학습을 진행하는 방식이다. 

주의사항 : learning rate를 기존의 1/10 만큼 조금 낮춰서 진행하자.

 경우에 따라서 학습 방법의 팁이 존재하니 참고하도록 하자. 데이터 수가 적고, 분류할 data가 기존의 모델에서 사용하던 label과 다르다면 문제가 크지만, 다양한 노력을 해보도록 하자.

 Object Detection 또는 Imager Captioning을 하는 경우, Transfer learning을 사용한다고 합니다. 그리고 각자의 목적에 맞도록 fine-tuning하는 것이다. 구체적으로 Object Detection은 시작이 CNN이므로 이 부분을 pretrain하며, Image Captioning은 Word Vectors를 pretrain한다고 합니다.

Summary

 

Reference

 

 

 

저작자표시

'CS231' 카테고리의 다른 글

Lecture 9 : CNN Architectures  (0) 2020.05.02
Lecture 8 : Deep Learning Software  (0) 2020.05.02
Lecture 6 : Training Neural Networks I  (2) 2020.04.12
Lecture 5 : Convolutional Neural Networks  (3) 2020.04.03
Lecture 4 : Backpropagation and Neural Networks  (0) 2020.03.29

관련글

댓글

티스토리툴바