"Training Neural Networks I"을 들어가기전 지금까지의 수업 내용을 잠깐 되돌아 보자.
 |
Overview (Training Neural Networks)
이번 장에서는 네트워크를 학습시키는 것과 관련한 부분을 다둘 것이다.
처음에 신경망을 어떻게 설정할 것인가? 어떤 Activation Function을 선택해야하는가? Data Preprocess 어덯게 해야할지? weight initiailzation, regularization, gradient checking 관련하여 학습이 동적으로 진행되는 관점에서 얘기해볼것이다. 아래는 신경망 학습에 필요한 초기 설정, 동적 학습, 평가로 3단계로 구분하여 정리한 것이다.
 |
Part 1
 |
이번 장에서 다룰 내용은 위와 같으며 하나하나씩 아래 다루고자 한다.
Activation Functions
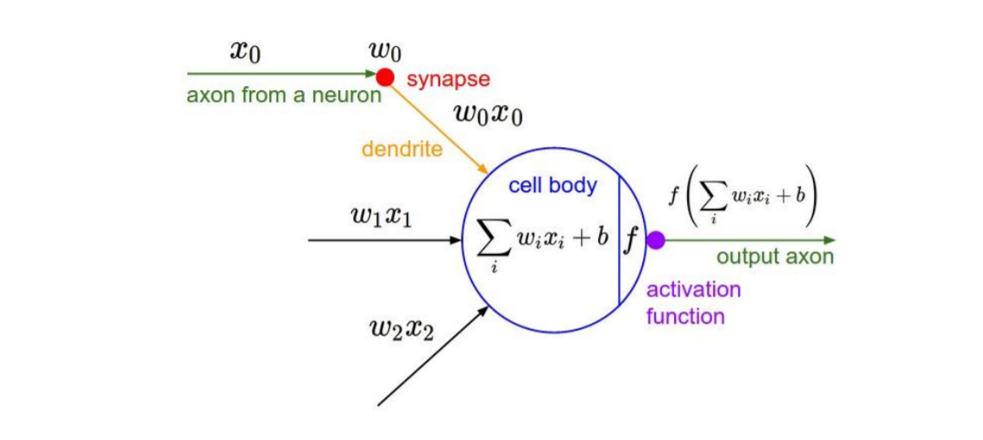 |
input data와 wight의 계산(곱)으로 얻어진 값을 Activation Functions(non linearity)에 넣어 output을 얻었다.
 |
그리고, 다양한 Activation Function을 봤었지만, 이 장에서는 각각의 Activation Function의 자세한 설명 및 서로의 trade-off를 확인해볼 예정이다.
1. Sigmoid
 |
Sigmoid function : 고전적으로 자주 사용하던 기법으로, input이 매우 크면 1로, 음수로 매우 작으면 0으로 값으로 가까워지게 만드는 함수이다. 그리고, 0 주변에서는 linear function처럼 보이게 된다.
하지만, Sigmoid의 경우 3가지의 문제점이 다음과 같이 존재한다.

|
첫째 : gradient(1차 미분값)을 소멸시키는 문제 발생 (아래, Sigmoid Function을 +inf, -inf, 0 에서의 gradient를 구하면 각각 0, 0 ,1/4 이다. (심지어, sigmoiod function의 gradient가 가장 클 것으로 예상되는 점 x=0 일때의 gradient가 1/4로 가장 큰 값, 문제!) 이를, gradient vanishing 현상으로 이루어진다.
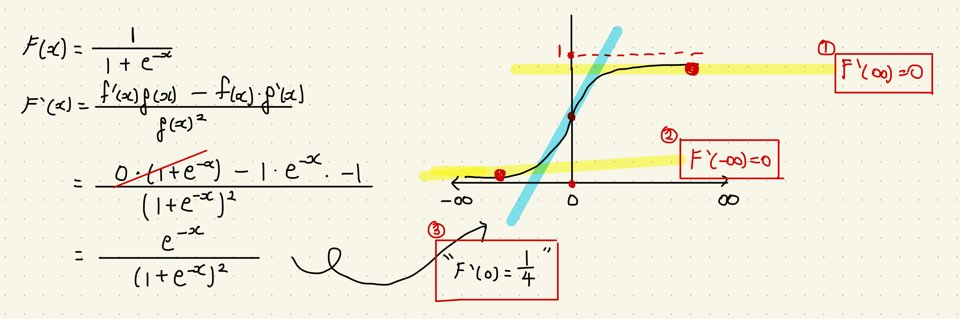 |
 |
 |

|
둘째 : sigmoid의 ouput이 0(output을 보면 0 ~ 1사의 값)을 중심으로 나오지 않는다. 즉, 학습이 느리다는 단점
 |
왜 이런 현상이 일어나는지 아래를 확인해보자.
 |
 |
셋째 : exp(-x) 연산은 복잡(연산 비용 높음)한 연산이므로, 속도가 느리다.
 |
지금까지 Sigmoid의 문제점을 정리하면 다음과 같다.
- 그라디언트가 죽는 현상이 발생한다 (Gradient vanishing 문제) gradient 0이 곱해 지니까 그다음 layer로 전파되지 않는다. 즉, 학습이 되지 않는다.
- 활성함수의 결과 값의 중심이 0이 아닌 0.5이다. (학습속도 느림)
- 계산이 복잡하다. (지수함수 계산)
다음은 sigmoid 함수의 zero-centered 문제점을 극복 하기 위해 Tanh 함수를 살펴보자
2. tanh(x)
 |
하지만, 아직도 gradient vanishing 문제와 exp 연산이 남아 있다는 문제점이 있다.
다음은 ReLU를 살펴보자.
3. ReLU
 |
ReLU의 장점은 다음과 같다.
- +(0보다 큰 구간)에서는 saturate하지 않는다.(기울기가 0에 수렴하지 않으므로, gradient vanishing 해결)
- exp(-x)가 없기 때문에, 계산이 보다 효율적임
- sigmoid / tanh보다 약 6배 빨리 수렴한다.
- 실제로, sigmoid보다 생물학적으로 그럴듯 하다.
하지만, ReLU 또한 문제점이 다음과 같이 있다.
 |
함수값이 0을 중심으로 나오지 않는것과 함수값이 0보다 작은 경우의 gradient를 보면 모두 0인게 문제점이다.
 |
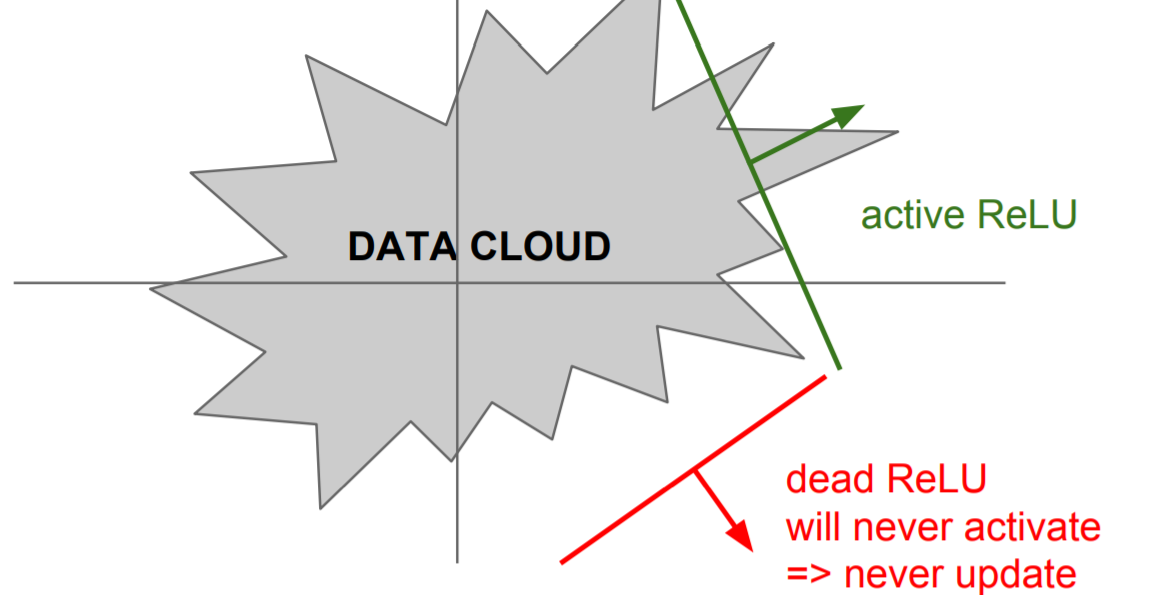 |
즉, 0보다 큰 함수값은 ReLU에 의해 활성화되지만, 0보다 작은 부분은 update가 되지 않는다. 이를 해결하고자 ReLU에서 0보다 작은 부분을 0으로 하지 않고 0.01을 곱해 아래와 같이 살짝 변경한것이 Leaky ReLU이다. (결국, activation function의 domain인 input 값이 어느 구간에서라도 죽지 않음)
 |
4. Learky ReLU
 |
5. PReLU(Parametric Reactifiler)
 |
추가적으로 0.01이 아닌 알파를 상수배 시킴으로써 보다 일반화 시킨 것이 PReLU라는 Activation Functions이다.
6. ELU (Exponetial Linear Units)
 |
7. Maxout
 |
최종 선택 방안 (Tips)
 |
주로, ReLU를 사용하지만, learning rate(학습률)을 고려하고, 학습이 잘 안된다면, Learky ReLU / Maxout / ELU 를 고려해보고, 이후에 tahn를 사용해보자(기대는 하지 말기), 그리고 절대로 sigmoid는 사용하지 말것!
Data Preprocessing (전처리)
 |
input data를 trainning 시키기 전에 preprocessing을 해주는 것은 이미지 처리 외에 다른 Machine Learning에서도 이루어지는 일이다.
그런데 우리는 왜 preprocessing 하는건지 물어보면 답을 못하는 경우도 있다.
 |
이 강의의 경우. 앞서 sigmoid function의 문제점인 zero-centering 못하는 문제점을 연결해서보면 input x의 부호에 따라 gradient가 의존하기 때문에, 수렴속도가 느리다는 단점이 있었는데, input data를 학습전에 zero-centered data로 preprocessing을 함으로 수렴속도를 개선시킬 수 있으므로 필요성을 강조한다.
그리고, normalized는 특정 범위 안으로 값들을 모아 놓은 것이다. (이미지 처리에서는 nomalized 사용 X. 이유 : 0 ~ 255라는 값이 이미 pixel 값으로 정해져 있으므로, zero-centering 사용 O)

|
그리고, PCA, Whitening 기법을 통해 Preprocessing 시키는 방안도 있지만, CNN에서는 이런 변환을 사용하는 경우가 거의 없다.
 |
흔히 하는 실수 : 전처리 기법을 적용함에 있어서 명심해야 하는 중요한 사항은 전처리를 위한 여러 통계치들은 학습 데이터만 대상으로 추출하고 검증, 테스트 데이터에 적용해야 한다. 예를 들어 평균차감(mena subtraction) 기법을 적용 할 때 흔히 하는 실수 중에 하나는 전체 데이터를 대상으로 평균차감 처리를 하고 이 데이터를 학습, 검증, 테스트 데이터로 나누어 사용하는 것이다. 올바른 방법은 학습, 검증, 테스트를 위한 데이터를 먼저 나눈 후에 학습 데이터를 대상으로 평균값을 구한 후에 평균차감 전처리를 모든 데이터군(학습, 검증, 테스트)에 적용하는 것이다.
Weight Initialization (가중치 초기화)
 |
Q1) 처음에 W가 0이면 어떻게 될까?
A1) 가중치가 0으로 초기화된 신경망 내의 뉴런들은 모두 동일한 연산 결과를 낼 것이고 따라서 backpropagaton 과정에서 동일한 그라디언트(gradient) 값을 얻게 될 것이고 결과적으로 모든 파라미터(paramter)는 동일한 값으로 업데이트 될 것이기 때문이다. 다시말해, 모든 가중치 값이 동일한 값으로 초기화 된다면 뉴런들의 비대칭성(asymmetry)를 야기할 요소가 사라지게 된다.
위의 문제점을 해결하고자 First Idea는 다음과 같다.
 |
위에서 언급한 이야기를 종합하자면, 가중치 값은 가능한 0에 가까운 값이어야 또한 모든 동일하게 0이되어서는 안된다는 것이다. 소위 symmetry breaking을 사용하는데 이는 0에 가까운 (하지만 0이 아닌) 값으로 가중치를 초기화시키는 방법이다. 즉, 모든 가중치들을 난수를 이용하여 고유한 값으로 초기화 함으로써 각 파라미터 값이 서로 다른 값으로 업데이트 되고 결과적으로 전체 신경망 내에서 서로 다른 특성을 보이는 다양한 부분으로 분화될 수 있다. 평균이 0, 표준편차가 1인 가우시안 분포를 따르는 랜덤값에 0.01을 곱함으로써 W를 만든다. 운이 좋게도 층이 얇은(작은 Network)에서는 잘 먹히지만, 층이 깊은 신경망에서는 문제가 발생하게 된다.
주의 : 가중치를 0에 가까운 작은 값으로 초기화 하는 것은 항상 좋은 성능을 답보하는 것은 아니다. 예를들어 아주 작은 값으로 구성된 가중치 값으로 된 신경망의 경우 backpropagation 연상 과정에서 그라디언트(gradient) 또한 작은 값을 갖게 된다(그라디언트(gradient)는 가중치 값에 례하기 때문). 이는 네트워크의 역방향으로 흐르며 전달되는 “그라디언트 시그널(gradient signal)”을 감소시키게 되고 이는 신경망 학습에 있어서 중요한 문제를 야기하게 된다.
가중치를 표준편차가 0.01인 정규분포로 초기화할 때의 각 층의 활성화(tanh)값 분포
은닉층의 활성화값의 분포를 관찰하면 중요한 정보를 얻을 수 있다.
- 10개의 층
- 각각의 층에는 500개의 뉴런 설정
- 활성화 함수 : tanh(Wx+b)
- first init : 0.01 * np.random.randn(D, H)
 |
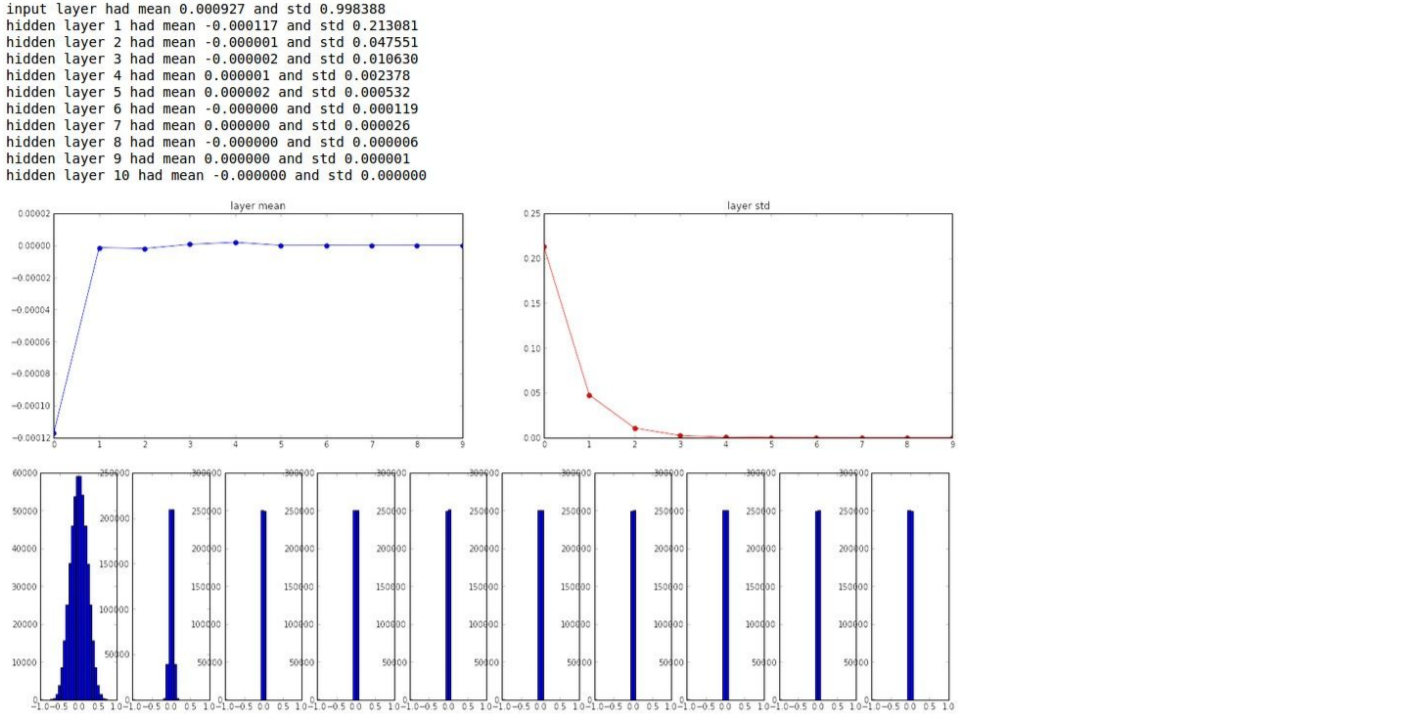 |
임의로 생성한 입력 데이터를 위 가중치에 대입하였더니, 1-Layer를 지난 활성화값은 평균이 0, 분산이 다소 있는 히스토그램이 그려지지만, 2,3,..10-Layer로 깊어질수록 활성화함수 값이 평균은 0이지만, 분산이 거의 없는 히스토그램을 보여주고 있다.
 |
결과 해석 : 활성화 값이 0.0에 치우쳤다는 것은 표현력 관점에서는 큰 문제가 있는 것이다. 즉, 다수의 뉴런이 거의 같은 값을 출력하고 있으니 뉴런을 여러 개 둔 의미가 없어진 것이다. 예를 들어 뉴런 500개가 거의 같은 값을 출력한다면 뉴런 1개짜리와 볆반 다를 게 없는 것이다. 그래서 활성화값들이 치우치면 표현력이 제한된다는 관점에서 문제가 된다.
가중치를 표준편차가 1인 정규분포로 초기화할 때의 각 층의 활성화(tanh)값 분포
다음은 초기값 설정 시, 0.01이 아닌 1로 설정하여 위와 동일한 실험을 해보자.
- 10개의 층
- 각각의 층에는 500개의 뉴런 설정
- 활성화 함수 : tanh(Wx+b)
- first init : 1.0 * np.random.randn(D, H)
 |
결과 해석 : 활성화값들이 0과 1에 치우쳐 있는데, 여기에서 사용한 tanh 함수는 그 출력이 0에 가까워지자(또는 1에 가까워지자) gradient는 0에 다가간다. 그래서 데이터가 0과 1에 치우쳐 분포하게 되면 역전파의 기울기 값이 점점 작아지다가 사라지게 된다. 이것이 기울기 소실(Gradient Vanishing)이라 알려진 문제이다. 층을 깊게 하는 딥러닝에서는 기울기 소실은 더 심각한 문제가 될 수 있다.
가중치의 초깃값으로 'Xavier 초깃값'을 이용할 때의 각 층의 활성화(tanh)값 분포
- 10개의 층
- 각각의 층에는 500개의 뉴런 설정
- 활성화 함수 : tanh(Wx+b)
- first init : np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)
예시 : Xavuer 초깃값
 |
 |
결과 해석 : 층이 깊어지면서 형태가 다소 일그러지지만, 앞에서 본 방식보다는 확실히 넓게 분포됨을 알 수 있다. 각 층에 흐르는 데이터는 퍼져 있으므로, tanh 함수의 표현력도 제한받지 않고, 학습이 효율적으로 이뤄질 것으로 기대된다.
지금까지 위에서의 tanh 함수는 좌우 대칭이라 중앙 부근이 선형인 함수로 볼 수 있었다. 그래서 Xavier 초깃값이 적당하여 바로 위의 결과가 잘 나왔었다. 하지만 ReLU를 사용하면 어떤 결과가 나올지 다음 실험 결과를 확인해보자.
가중치의 초깃값으로 'Xavier 초깃값'을 이용할 때의 각 층의 활성화(ReLU)값 분포
- 10개의 층
- 각각의 층에는 500개의 뉴런 설정
- 활성화 함수 : ReLU(Wx+b)
- first init : np.random.randn(fan_in, fan_out) / np.sqrt(fan_in)
 |
결과 해석 : 층이 깊어지면서 치우침이 조금씩 커지게 된다. 실제로 층이 깊어지면 활성화값들의 치움치도 커지고, 학습할 때 "기울기 소실" 문제를 일으킬 것이다.
가중치의 초깃값으로 'He 초깃값'을 이용할 때의 각 층의 활성화(ReLU)값 분포
- 10개의 층
- 각각의 층에는 500개의 뉴런 설정
- 활성화 함수 : ReLU(Wx+b)
- first init : np.random.randn(fan_in, fan_out) / np.sqrt(fan_in/2)
 |
결과 해석 : 모든 층에서 균일하게 분포한다. 층이 깊어져도 부노가 균일하게 유지되기 때문에 역전파 때도 적절한 값이 나올 것으로 기대할 수 있다.
He 초깃값은 표준편차가 sqrt(2/fan_in) 인 정규분포를 사용한다. ReLU는 음의 영역이 0이라서 더 넓게 분포시키기 위해 2배의 계수가 필요하다고 (직감적으로) 해석할 수 있다.
추가적으로 가중치 초기화와 관련하여 선행 연구 자료들을 참고하자.
 |
Batch Normalization (배치 정규화)
 |
앞절에서는 각 층의 활성화값 분포를 관찰해보며, 가중치의 초깃값을 적절히 설정하면 각 층의 활성화값 분포가 적당히 퍼지면서 학습이 원할하게 수행됨을 알았다. 그렇다면 각층이 활성화를 적당히 퍼뜨리도록(신경망 학습단계에서 activation 값이 표준정규분포를 갖도록) "강제"해보면 어떨까? 실은 "배치 정규화"가 그런 아이디어에서 출발한 것이다.
Internal Covariate Shift 의미
 |
 |
Internal Covariate Shift란?, 신경망이 깊어질수록 각 Layer를 지날때마다 활성화값의 분포가 점점 한쪽으로 치우치는 현상을 의미한다. 이는 학습과정을 방해하는 요인이며, 이를 극복하고자 분포가 고르도록 정규화를 시키는 것이다.
 |
batch로 들어오는 신경망 각 Lyaer에 input의 분포를 평균 0, 표준편차 1인 분포로 만들어버리는 것.
- N : training examples in current batch
- D : Each batch's dimension
CNN에서는 activation map마다 하나씩 BN 진행 (확인 필요)
Batch Normalization : 위 처럼 N x D의 input(batch)이 새로운 뉴런으로 들어오면 이 batch가 들어오면 이걸 Normalize(평균 0, 표준편차 1)한다는 것이다.
 |
배치 정규화가 가능한 이유는 단순 미분 가능한 연산이었기에 적용 가능하다. 실제 구현에서는 배치 정규화 레이어를 "FC-Layer" or "Convolutional-Layer" 뒤 또는 "non-liner"(e.g. tanh) 연산 이전에 위치 시키는 방식으로 이 기법을 신경망에 적용할 수 있다.
 |
문제점 : 반드시 tanh-layer에 Unit gaussian input이 필요합니까? (각 layer의 출력값을 비슷한 분포로 생성(Unit Gaussian))
Scale과 Shift를 해주는 이유
 |
학습을 진행하면서 감마와 베타를 찾게 된다. 즉 학습을 통해서 BN을 어느정도로 할 것인가 결정한다.
위의 식에서 입력 데이터에 대해 정규화를 해주게 되면, 대부분의 값이 0에 가까워질 것이다. 이상태에서 활성화함수(e.g. ReLU)에 들어가게 된다면, 0 이하의 값들은 모두 0이므로, 앞에서 기껏 정규화를 했지만 의미가 없어져 버리게 된다. 따라서, 정규화된 값에 Scale 및 Shift를 계산하여 ReLU가 적용되더라도 기존의 음수 부분이 모두 0으로 되지 않도록 방지해 주고 있다. 물론 이 값은 학습을 통해서 효율적인 결과를 내기 위한 값으로 찾으므로 걱정할 필요는 없다.
 |
배치 정규화 장점
- 학습을 빨리 진행할 수 있다. (학습 속도 개선)
- 학습률이 높아도 괜찮다. (Robust)
- 초깃값에 크게 의존하지 않는다. (골치 아픈 초깃값 선택 장애여 안녕!)
- 오버피팅을 억제한다. (드롭아웃 등의 필요성 감소)
테스트(추론) 단계에서의 BN
 |
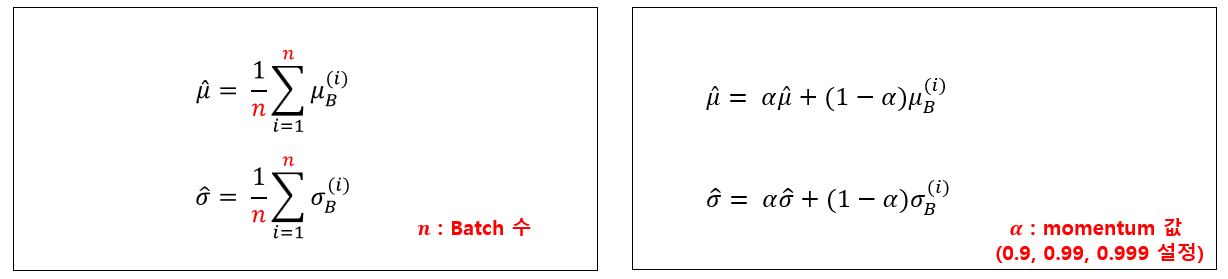
Test 단계(Train 단계처럼 데이터가 하나씩 주입된다고 가정)나 Test 단계에서는 평균과 표준편차를 계산할 미니배치가 없기 때문에 전체 Training Set의 평균과 표준편차를 사용한다. 하지만, 엄청나게 많은 전체 Training set에 대한 평균과 표준편차를 계산하기에는 무리기 때문에, 아래 (좌)의 식과 같이 각개의 미니배치에 대한 평균과 표준편차를 이용해 전체 Training Set의 평균과 표준편차를 대신한다. 또는 아래 (우)의 식과 같이 train 단계에서 지수 감소(exponential decay) 이동 평균법(moving average)을 사용하여 평균과 표준편차를 계산할 수 있다.
 |
아래 예제를 통해 Batch Normalization의 의미를 직관적으로 확인
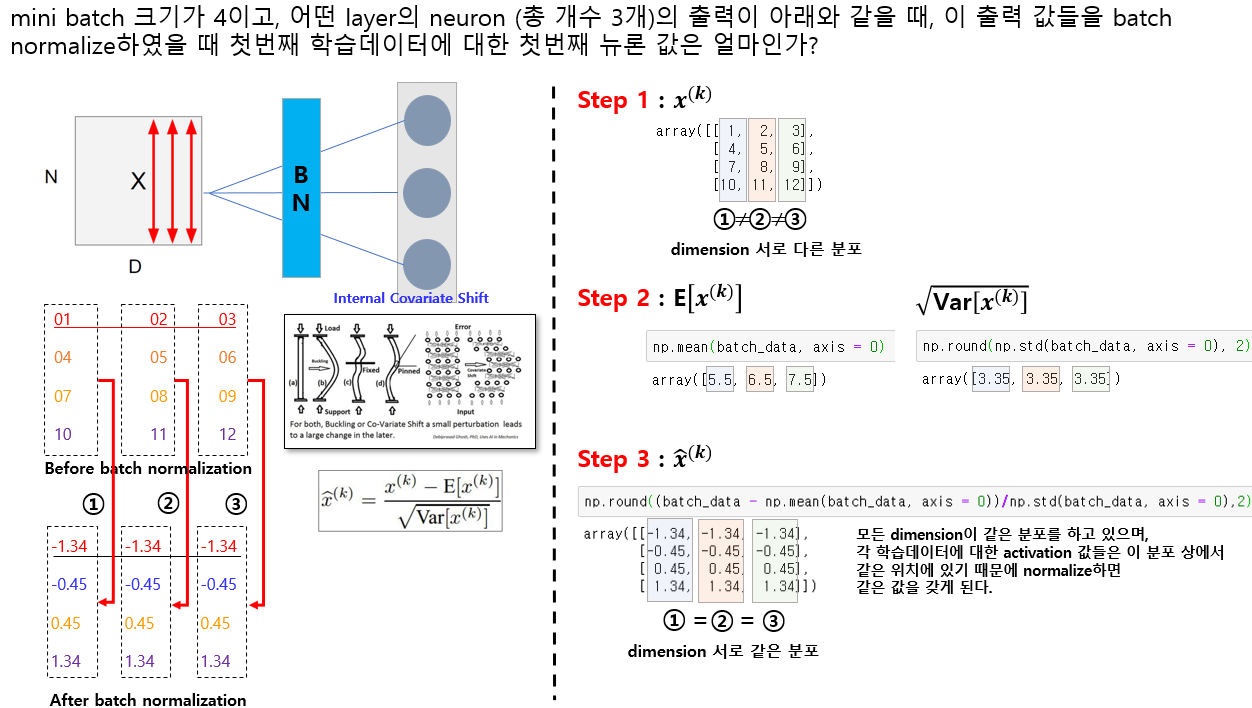 |
BN을 적용함으로써 Layer에 들어가는 입력 값들의 dimension에 따른 normalize distribution로 변경시켜주고 있다. 따라서 Internal Covariate Shift를 막아주는 역할을 한다.
Babysitting the Learning Process (학습 과정을 살펴보자!)
- Preprocess the data (데이터 전처리)
- Choose the architecture (신경망 구조 선택)
- Double check that the loss is reasonable (Loss가 합리적인 것인지 이중 확인)
 |
 |

|
loss가 잘 나오는지 확인해보자! 3강에서 다룬 softmax의 loss가 -log(x) 였다. 하지만, regularization을 0으로 설정하면 - log(1/class)이므로, 2.3인 것을 확인할 수 있다.
 |
regularization의 값을 살짝 올렸을 때, Loss가 증가된 것을 확인할 수 있다. 이는 Layer가 동작하는지 확인하는 sanity check라고 한다.
 |
본격적으로 훈련을 시켜보자. 모든 데이터를 넣지 말고 일부만 가지고 진행해보자.
 |
loss가 아주 작아지며, train data의 정확도가 100%임을 확인하였고, 이런 오버피팅이 제대로 되고 있으면 모델이 동작한다는 것을 의미한다.
loss가 내려가는 적당한 samll regularization 과 learning rate를 찾기
-
learning_rate : 1e-6
 |
결과 해석 : cost(loss)의 변화가 거의 없기 때문에, 이는 아마도 learning_rate가 지나치게 낮게 설정되어 있기 때문이다. 추가적으로 train/val의 정확도는 약 20%이다. (이유 : 아무리 learning_rate가 작아도 훈련은 진행중이기 때문)
 |
- learning_rate : 1e+6
 |
 |
결과 해석 : cost(loss)가 NaN이 나오고 있다. 이는 learning_rate가 지나치게 높게 설정되어 있기 때문이다.
- learning_rate : 3e-3
 |
결과 해석 : cost(loss)가 잘나오다가 epoch 5부터 NaN이 나오고 있다. 이는 learning_rate가 지나치게 높게 설정되어 있기 때문이다.
여기서 1e-3 ~ 1e-5값이 적당하다라는 것을 추측할 수있다. 이렇게 learning_rate를 찾아야한다.
Hyperparameter Optimization (하이퍼파라미터 최적화)
신경망에는 하이퍼파라미터가 다수 등장한다. 여기서 말하는 하이퍼파라미터는 각 층의 뉴런 수, 배치 크기, 매개변수 갱신 시의 학습률과 가중치 감소 등이다. 이러한 하이퍼파라미터의 값을 적절히 설정하지 않으면 모델의 성능이 크게 떨어지기도 한다. 하이퍼파라미터의 값은 매우 중요하지만 그 값을 결정하기까지는 일반적으로 많은 시행착오를 겪는다. 여기서는 하이퍼파라미터를 최대한 효율적으로 탐색하는 방법을 설명한다.
 |
주의할 점 : 하이퍼파라미터의 성능을 평가할 때는 시험 데이터를 사용해서는 안 된다.
시험 데이터를 사용하여 하이퍼파라미터를 조정하면 하이퍼파라미터 값이 시험 데이터에 오버피팅되기 때문이다. 범용 성능이 떨어질 수 밖에 없다.
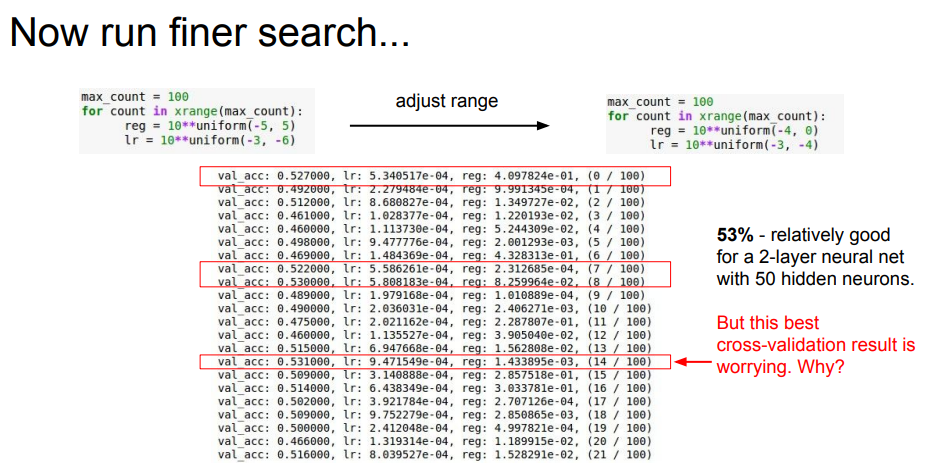
하이퍼파라미터의 범위는 "대략적으로" 지정하는 것이 효과적이다. 실제로도 0.001에서 1000사이와 같이 "10의 거듭제곱" 단위로 범위를 지정한다. 이를 "로그 스케일로 지정"하는 것이다.
 |
 |
 |
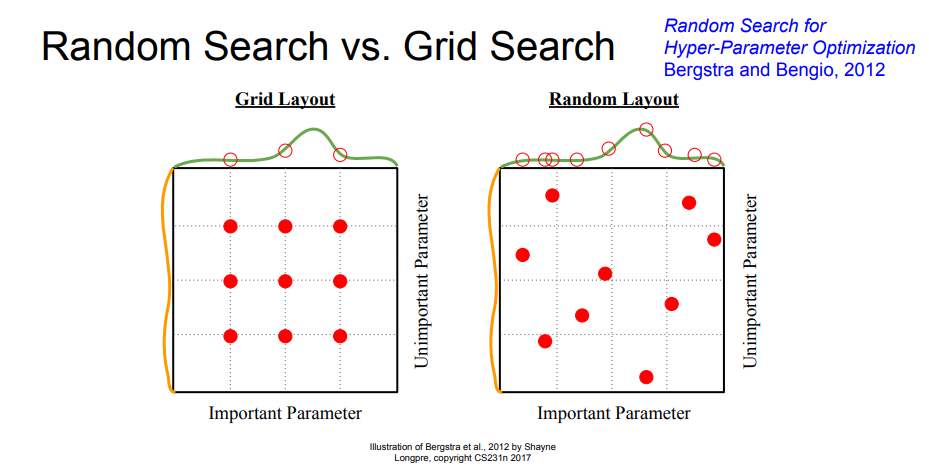 |
NOTE : 신경망의 하이퍼파라미터 최적화에서는 그리드 서치같은 규칙적인 탐색보다는 무작위로 샘플링해 탐색하는 편이 좋은 결과를 낸다고 알려져 있다. 이는 최종 정확도에 미치는 영향력이 하이퍼파라미터마다 다르기 때문이라고 한다.
 |
 |
 |
 |
 |
 |
'CS231' 카테고리의 다른 글
| Lecture 8 : Deep Learning Software (0) | 2020.05.02 |
|---|---|
| Lecture 7 : Training Neural Networks II (2) | 2020.04.16 |
| Lecture 5 : Convolutional Neural Networks (3) | 2020.04.03 |
| Lecture 4 : Backpropagation and Neural Networks (0) | 2020.03.29 |
| Lecture 3 : Loss Functions and Optimization (0) | 2020.03.22 |



댓글