2020-2학기 서강대 김경환 교수님 강의 내용 및 패턴인식 교재를 바탕으로 본 글을 작성하였습니다.
Ch7.4까지는 물리학의 영감을 받은 classifier를 다뤘었다. 이번 Ch7.5에서는 생물학적 진화의 과정에 영감을 받아서, classifier 설계를 하고자 한다.
7.5 Evolutionary methods (적자생존)
분류기 설계의 진화적 방법들은 최적 분류기를 위해 Stochastic Method(탐색)를 사용한다. 이 방법들은 대규모 병렬 컴퓨팅에 적합하다.
▶ Inspired by the biological evolution
- employing stochastic search for an optimal classifier
- occasional very large changes in the classifier are introduced.
▶ steps
- creating several classifiers – a population – each varying somewhat from the other
- scoring each classifier on a representative version of the classification task (fitness)
- ranking the classifiers according to their score and retain the best classifiers (survival of the fitness)
- the entire process is repeated for generations
조금 더 내용을 추가하면 아래의 step으로 진행된다.
- 몇 개의 서로 다른 classifier를 만든다. – a population(집단) –
- label이 붙은 samples의 집합에 대한 정확도 같은 분류 작업을 진행하여 scoring을 한다. 생물학적 진화와의 유사성을 유지하기 위해, 결과 점수(scalar)를 때때로 적응도 (fitness)라고 부름
- classifier들을 그들의 점수에 따라서 순위를 메기고 전체 집단의 일부인 최선의 classifier를 남긴다. (적자생존)
- 그 다음 세대 – the children or offspring(자식) – 을 만든다. 어떤 자식 classifier들은 그들의 이전 세대 부모보다 더 높은 점수를 가질것이며, 일부는 더 낮은 점수를 가질 것이다.
- 전체 프로세스가 다음 세대를 위해 반복됨.
classifier들은 채점되며, 최선의 classifier들만 남고, 또 다른 세대를 제공하기 위해 랜덤하게 변경되고, 기타 등등. 부분적으로는 순위 때문에 각 세대는 평균적으로 이전 세대보터 얀간 더 높은 점수를 가진다. 이 프로세스는 어떤 세대에서 단 하나의 최고 classifier가 원하는 기준 값을 초과하는 점수를 가질 때 정지된다.
▶ Genetic Algorithms
chromosome (염색체)
- the fundamental representation of each classifier (각 classifier를 염색체라고 불리는 2진 문자열)
- the mapping from the chromosome to the features and other aspects of the classifier depends on the problem domain. (염색체로부터 특징들, classifier의 다른 양상들로의 매핑은 문제 도메인에 종속되며, 설계자는 이 매핑을 규정하는 데 큰 허용 범위를 가짐)
pattern classifer에서 socre(점수)는 보통 데이터 집합에 대한 정확도의 어떤 단조 함수로 선정된다. 이때 overfitting을 피하기 위해 penalty 항을 추가할 수도 있다. 여기서 fiteness(적응도) $\theta$를 stop criterion(정지 기준)으로 사용할 것이다. 깊게 다루기 전에, 우선 기본적 유전자 알고리즘의 구조를 더 구체적으로 다루고, 알고리즘에서 사용되는 유전자 연산자들의 핵심 개념을 알아보자.
교재의 번역이 어색한 부분이 있어 보다 직관적인 이해를 위해 알고리즘과 예제를 살펴보는게 좋을것 같다. (아래)
- $\theta$ : 정지 기준 (stop criterion)
- $P_{co}$ : 교차 확률
- $P_{mut}$ : 돌연변이 확률
- $L$ : classifer 갯수

Genetic operators (유전자 연산자)
위 Basic Genetic Algorithm의 Line [5 ~ 7]에서 일어나는 과정을 유전자 연산이 일어나며, 아래 세 개의 연산자가 있다.
<영어 교재>
- Replications (복제) : a chromosome is merely reproduced, unchanged.
- Crossover (교차) : mixing/mating of two chromosomes. A split point is chosen randomly along the length of either chromosome. Pco is the probability a given pair of chromosomes will undergo crossover.
- Mutation (돌연변이) : each bit in a single chromosome is given a small chance, Pmut, of being changed from a 1 to a 0 or vice versa.
<한글>
- Replications (복제) : 염색채는 단지 재생산되며, 바뀌지 않는다.
- Crossover (교차) : 두 개의 염색체의 교배를 뜻하며, 한 분리 점이 염색체의 길이 방향에서 랜덤하게 선정된다. 염색체 $A$의 앞부분은 염색체 $B$의 뒷부분과 접합되며, 그 역도 마찬가지로 접합되어, 두 개의 새로운 염색체가 만들어 진다. 주어진 염색체 쌍이 교차될 확률은 알고리즘 4의 $P_{co}$로 주어짐.
- Mutation (돌연변이) : 한 염색체의 각 bit에서는 1에서 0으로, 또는 0에서 1로 변할 작은 확률 $P_{mut}$가 주어짐

이외에도 다른 유전자 연산자도 존재한다. 예를 들어, 염색체 앞뒤가 뒤바뀌는 inversion(도치). 이 연산자는 높은 점수의 염색체를 도치시키면 거의 항상 낮은 점수의 염색체로 바뀌기 때문에 매우 드물게 사용.
아래 예제는 기본적 유전자 알고리즘의 이해를 돕고자 첨부함 (유전자 연산자 포함)
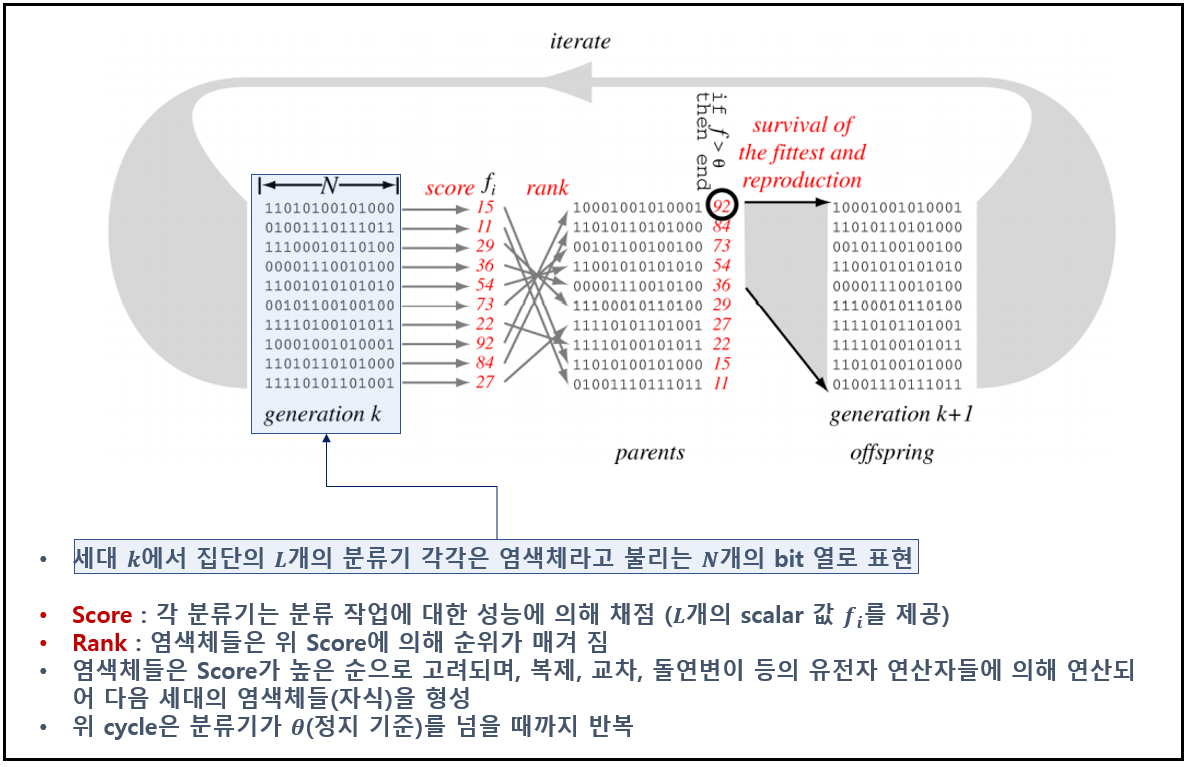
▶ A Simple Genetic Algorithm (위 예제를 작은 문제로 만들어 보다 상세하게 풀이)
- GAs require the natural parameter set of the optimization problem to be coded as a finite-length string over some finite alphabet.
- $f(x) = x^2$ on the integer interval [0, 31]
- A back of five input switchs - a way to code the parameter $x$.
- The objective of the problem is to set the switches to obtain the maximum possible $f$ value.
원래는 $f(x)$를 모르지만 문제의 이해를 돕기 위해 $f(x)$를 안다고 가정하자.
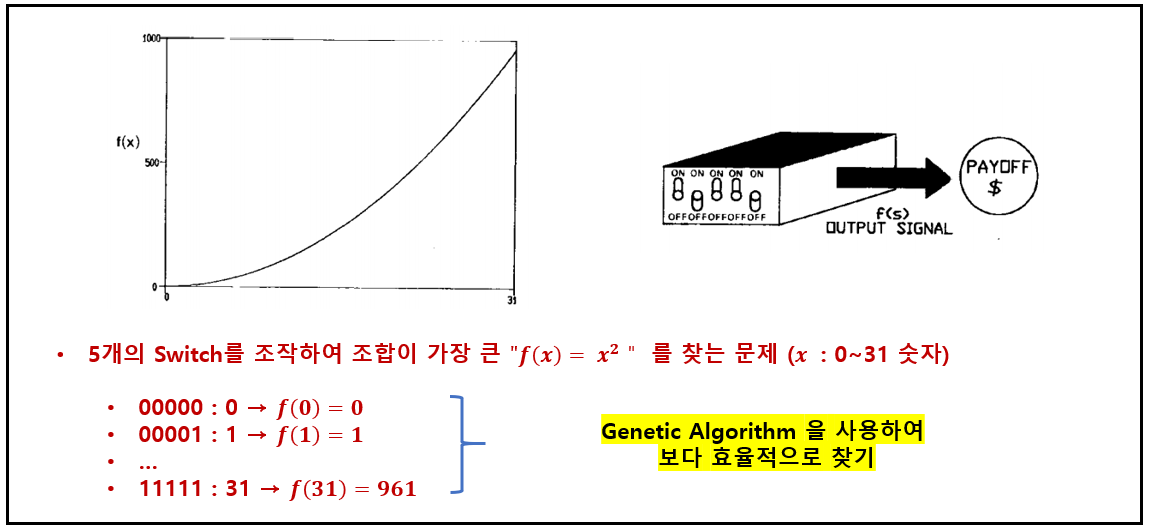
object : $f(x)$를 모를 때 $f(x)$를 최대로 하는 5개의 switch (2bit)는 어떤 array로 존재할까?
- The initial population was chosen at random through 20 successive flips of an unbiased coin.
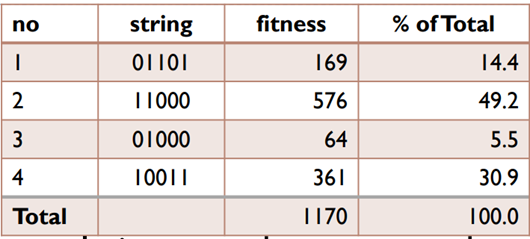
- fitness of no.1 : $ 0 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 1 = 169$
- % of Total of no.1 : $\frac{169}{1170} = 14.4$%
reproduction 하는 경우 "weighted roulette wheel"을 사용하는데, 이때의 weight는 위에서 구한 fitness(score)의 상대비율에 따라 다음 복제를 한다. (no.1의 "01101"이 reproduction될 확률은 $14.4%$로 아래 룰렛에서의 면적 ①로 주어져있다. (즉 reproduction할때 아래의 룰렛을 돌려 나온 결과를 반영)
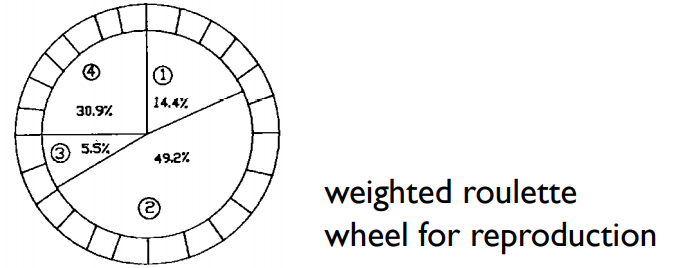
- We now must define a set of simple operations that take this initial population and generate successive populations that improve over time.
- Reproduction (weighted roulette wheel for reproduction)
- Crossover
- Mutation
위 개념은 위에서 설명했으니 생략하고, 예제를 보자.

Mutation은 아주 적은 확률적으로 일어나기 때문에, 위 예제에서는 반영되지 못한 것으로 새로운 세대가 Mutation 없이 Crossover의 결과와 동일하게 나온것으로 볼 수 있다.
Reference
'Pattern Classification [수업]' 카테고리의 다른 글
| Ch9.3 Algorithm-independent machine learning - Bias and variance (3) | 2020.12.09 |
|---|---|
| Ch9.1~9.2 Algorithm-independent machine learning - Introduction (0) | 2020.12.01 |
| Ch7.3 Stochastic Methods - Boltzmann learning (0) | 2020.11.25 |
| Ch7.2 Stochastic Methods - Stochastic search (0) | 2020.11.17 |
| Ch7.1 Stochastic Methods - Introduction (0) | 2020.11.17 |



댓글