2020-2학기 서강대 김경환 교수님 강의 내용 및 패턴인식 교재를 바탕으로 본 글을 작성하였습니다.
앞 Ch7.2 에서는 $w$가 fix된 상태에서의 최적의 $E$를 찾기 위한 각 unit의 state를 찾는 방법을 다뤘었다. 이번 Ch7.3에서는 적절한 $w$를 찾기 위한 방법을 논하고자 한다.
7.3 Boltzmann learning
패턴 인식을 위해 [그림 1]에 제시된 네트워크 구조를 사용하고자 한다. 네트워크는 다음과 같다.
▶ The network
- the input units accept binary feature information (2진값, 0 또는 1)
- the output units represent the output categories (1-of-c, node(unit)의 갯수 = class category 갯수)
- during classification, the input units are held fixed (or clamped) to the feature values of the input pattern; the remaining units are annealed to find the lowest-energy.
classification 하는 동안 input unit(node)들의 state를 fix(or clamped)하고, 나머지 unit(node)들은 최저 $E$의, 가장 확률 높은 구성을 찾기 위해 annealing을 한다.
보다 정확한 인식을 위해 적절한 $w$(가중치)를 필요로 하며, 따라서 train pattern으로부터 $w$를 학습하기 위한 방법을 시작한다.

▶ Stochastic Boltzmann learning of visible states
"KL Divergence" 내용 추가 필요


▶ Stochastic learning of input-output associations
input(입력)으로부터 output(출력)으로의 mapping들을 학습하는 문제를 고려하자. 다음 아래의 Network가 주어졌을 때, $\alpha^i$로 표기된 input unit들의 state(상태)와 $\alpha^o$로 표기된 output unit 들의 state간의 연관성을 학습하기를 원한다. 여기서의 적합한 비용 함수는 각 입력 패턴의 확률로 가중된 Kullback-Leibler 발산이다.
$$ \overline{D}_{KL} (Q(\alpha^o|\alpha^i), P(\alpha^o|\alpha^i)) = \sum_{\alpha_i}P(\alpha^i)\sum_{\alpha_o}Q(\alpha^o|\alpha^i)log\frac{Q(\alpha^o|\alpha^i)}{P(\alpha^o|\alpha^i)} \tag{1}\label{1}$$
식 (1)에서와 같이, 학습은 이 가중된 거리를 줄이기 위해 가중치들을 바꾸는 것을 포함한다.
$$\Delta w_{ij} = - \eta \frac{\partial \overline{D}_{KL}}{\partial w_{ij}} \tag{2}\label{2}$$
위 식은 즉, input unit이 학습 및 비학습 요소들 모두에서 fix되어 있다는 것이다. 그 결과는 가중치 갱신이 다음과 같다.
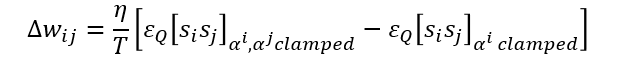


Reference
'Pattern Classification [수업]' 카테고리의 다른 글
| Ch9.1~9.2 Algorithm-independent machine learning - Introduction (0) | 2020.12.01 |
|---|---|
| Ch7.5 Stochastic Methods - Evolutionary methods (0) | 2020.12.01 |
| Ch7.2 Stochastic Methods - Stochastic search (0) | 2020.11.17 |
| Ch7.1 Stochastic Methods - Introduction (0) | 2020.11.17 |
| Ch5.3 Linear Discriminant Functions - Generalized linear discriminant functions (0) | 2020.11.02 |



댓글