2020-2학기 이화여대 김정태 교수님 강의 내용을 바탕으로 본 글을 작성하였습니다.
Overview
- Linear regressoin (MLE)
- Bias-Variance Decomposition
- Bayeisan linear regression
- Bayesian model comparison
- The evidence approximation
- Limit, of fixed basis functions
Bias variance decomposition
앞에서는 MLE를 이용하는 경우 overfitting이 발생한다는 단점이 있었다. 베이지안 방법론을 바탕으로 각각의 매개변수들을 주변화할 경우에는 overfitting이 발생하지 않는다. 이번 장에서는 베이지안 관점에서의 모델 복잡도에 대해서 더 깊이 살펴보려 한다. 그 이전에 빈도주의 관점의 모델 복잡도를 살펴보는 것이 도움이 되므로, Bias variance trade off (편향 분산 트레이드 오프)를 살펴보자.
regression problem의 결정 이론에 대해 논의할 때 조건부 분포 $p(t|\mathbf{x})$가 주어졌을 경우 해당 최적 예측값에 도달하도록 하는 다양한 오류 함수에 대해 살펴보았다. 가장 많이 사용되는 오류 함수는 제곱 오류 함수이며, 이 경우 최적의 예측치 $h(\mathbf{x})$는 조건부 기댓값 식 (1)로 주어지게 된다.
- The optimal estimator
$$h(\mathbf{x}) = E[t|\mathbf{x}] = \int t p(t|\mathbf{x}) d t \tag{1}\label{1}$$
- The loss function
$$ E(L) = \int \{y(\mathbf{x}) - h(\mathbf{x})\}^2 p(\mathbf{x}) d \mathbf{x} + \iint \{h(\mathbf{x}) - t \}^2 p(\mathbf{x}, t) d\mathbf{x} dt \tag{2}\label{2}$$
Ch1 (Loss function for regression)에서 기대 제곱 오류를 위와 같이 적을 수 있음을 증명함
- The first error term depends on our estimation $y(\mathbf{x})$ but the second term does not depend on it
첫번째 term은 $y(\mathbf{x})$를 어떤 것을 선택하느냐에 따라 결정되고, 우리의 목표는 첫번째 항의 값을 최소화하는 $y(\mathbf{x})$를 찾아내는 것이다. 이 항은 음수가 될 수 없기 때문에 달성 가능한 최솟값은 0. 망냑 무한한 수의 데이터와 제한 없이 많은 계산 자원이 있다면 원칙적으로 $h(\mathbf{x})$를 찾을 수 있음, 그러나 실제로 데이터 집합 $D$는 유한한 숫자 $N$개의 데이터 포인트들만 있으므로, 정확하게 알 수 없음
두번째 term은 $y(\mathbf{x})$와는 독립적으로 데이터의 내재적인 noise로 부터 생겨난 것, 기대 오류값이 도달할 수 있는 가장 최소의 값임
- If we model $h(\mathbf{x})$ by $y(\mathbf{x}, \mathbf{w})$, then from Bayesian perspective the uncertainty in our model is expressed by the posterior distribution of $\mathbf{w}$.
만약, 매개변수 $\mathbf{w}$에 의해 결정되는 매개변수적 함수 $y(\mathbf{x}, \mathbf{w})$를 이용하여 $h(\mathbf{x})$를 모델링한다면 베이지안 관점에서 이 모델의 불확실성은 $\mathbf{w}$에 대한 사후분포를 통해 표현될 것이다.
- From the frequentist view point, the uncertainty in model is caused by data set $D$ which is used for point estimation
하지만, 빈도주의적 관점에서는 데이터 집합 $D$를 바탕으로 $\mathbf{w}$에 대한 점 추정을 할 것이다. 이 경우 이 추정치의 불확실성을 다음의 사고 실험을 통해서 해석해 볼 수 있다.
- The data set $D$, size of $N$, is assumed to be drawn form the distribution $p(\mathbf{t}, \mathbf{x})$.
분포 $p(\mathbf{t}, \mathbf{x})$로부터 독립적으로 추출한 데이터 집합들이 있고, 각 집합의 크기가 $N$이라고 하자. 주어진 어떤 데이터 집합 $D$에 대해서든 학습 알고리즘을 실행해서 예측 함수 $y(\mathbf{x};D)$를 구할 수 있음. 서로 다른 데이터 집합은 서로 다른 함수를 결괏값을 내놓을 것이고, 그에 따라 서로 다른 제곱 오류값을 가지게 될 것이다. 어떤 특정 학습 알고리즘의 성능은 각 데이터 집합에서의 결과를 평균을 내어 구할 수 있음
- The integrand of the first term
$$\{y(\mathbf{x};D) - h(\mathbf{x})\}^2 \tag{3}\label{3}$$
식 (2)의 첫 번째 항의 피적분 함수를 살펴보자. 특정 데이터 집합 $D$에 대해서 이는 식(3)의 형태를 띠게 된다. 이 값은 데이터 집합 $D$에 대해 종속적, 따라서 각 데이터 집합으로부터 구한 값들을 평균을 내어 사용할 수 있음. 괄호 안에 $E_D[y(\mathbf{x};D)]$값을 더하고 뺸 후 전개하면 다음을 얻을 수 있음
- Ensemble average of of the integrand
$$\{y(\mathbf{x};D) -E_D[y(\mathbf{x};D)] +E_D[y(\mathbf{x};D)] - h(\mathbf{x})\}^2 \tag{4}\label{4}$$
$D$에 대해 식 (4)의 기댓값을 구하고 마지막 항을 정리하면 다음과 같게 된다.
$$\begin{aligned} &E_{D}\left[(y(\mathbf{x} ; D)-h(\mathbf{x}))^{2}\right]=\underbrace{\left(E_{D}[y(\mathbf{x} ; D)-h(\mathbf{x})]\right)^{2}}_{\text {bias }^{2}}+\underbrace{E_{D}\left[\left(y(\mathbf{x} ; D)-E_{D}[y(\mathbf{x} ; D)]\right)^{2}\right]}_{\text {variance }}\\ &\begin{array}{l} \end{array} \end{aligned} \tag{5}\label{5}$$
- bias : 전체 데이터 집합들에 대한 평균 예측이 회귀 함수와 얼마나 차이가 나는지를 표현
- variance : 각각의 데티터 집합($D_i$)에서의 해가 전체 평균에서 얼마나 차이가 나는지를 표현 (민감도)

- Above expression is for a single input value $\mathbf{x}$
지금까지 단일 입력 변수 $\mathbf{x}$에 대해서만 고려했음. 이 전개식을 식 (2)인 기대 제곱 오류에 대입하면, 기대 제곱 오류가 다음과 같이 분해될 수 있다는 것을 확인할 수 있음
- The data set $D$, size of $N$, is assumed to be drawn form the distribution $p(\mathbf{x}, \mathbf{t})$.
$$\text{expected loss} = (\text{bias})^2 + \text{variance} + \text{noise} \tag{6}\label{6}$$
여기서 각각의 항은 다음과 같다.

참고 : 전개 과정 및 설명 I, 전개 과정 및 설명 II
- There is trade off between variance and bias
Example : 100 data sets of 25 data point with Gaussian basis functions with $h(x) = sin 2\pie x$.
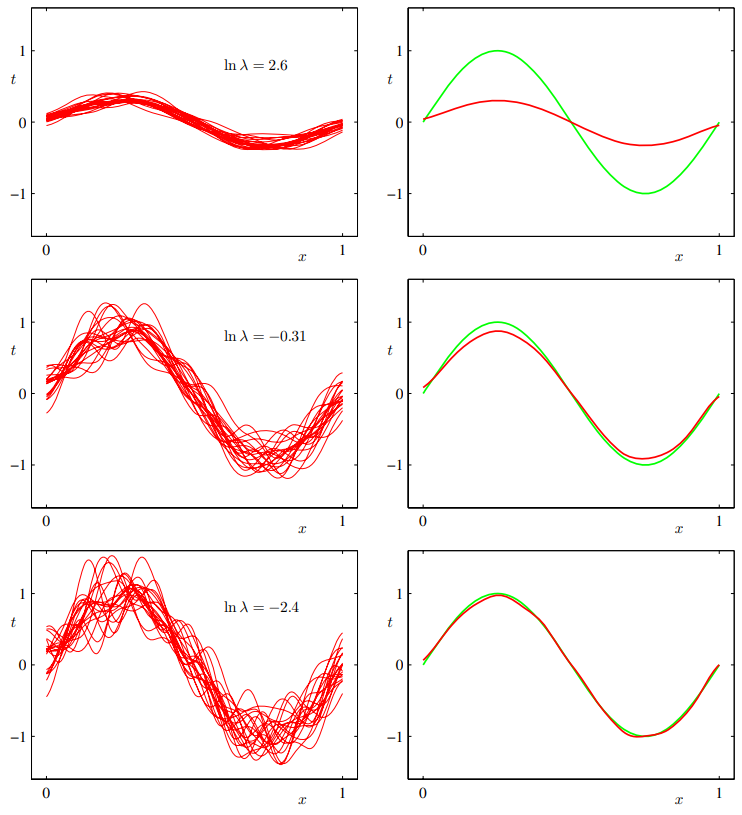
정규화 매개변수 $\lambda$에 의해 결정되는 모델의 복잡도가 bias 와 variance에 미치는 영향을 sign 곡선 데이터 집합을 이용하여 시각화함. $L=100$개의 데이터 집합들이 있으며, 각각의 집합은 $N=25$개의 데이터 포인트들을 가지고 있다. 모델은 24개의 가우시안 basis function을 바탕으로 구성되어 있음. 따라서 bias(편향) 매개변수까지 포함하면 모델의 총 매개변수 숫자는 $M=25$다. 왼쪽 그림은 다양한 값의 $\ln \lambda$에 대해서 데이터 집합들을 근사한 결과치가 그려져 있음 (100개 중 20개의 근사만을 그림). 오른쪽 그림은 100개의 해당 근사치들 평균(빨강)과 최초에 데이터 집합이 추출된 원래의 사인 삼수(녹색)을 그림
- A large value of regularization coefficient gives low variance but high bias
- For small $\lambda$, there is large variance but low bias
- Averaging many solutions of complex model is a very good fit, which suggests that averaging may be a beneficial procedure
- Weighted averaging of multiple solutions lies at the heart of Bayesian approach, although the averaging is with respect to the posterior distribution of parameters, not with respect to multiple data sets
실제로 여러 해들의 가중 평균을 내는 것은 베이지안 방법의 핵심에 해당한다. (베이지안 방법에서의 가중 평균은 여러 데이터 집합들데 대한 평균이 아니라 각 매개변수들의 사후 집합에 대한 것임?)
- Bias and variance plot
위 예시에 대해 variance-bias traed-off를 구체적으로 확인해보자. 평균 예측치는 다음으로 추정됨


- Although the bias variance decomposition may provide some insights, it is of limited practical use since it is based on ensemble average of data sets
편향 분산 분해를 통해 모델 복잡도의 문제에 대해서 빈도주의 관점의 흥미로운 통찰을 얻을 수 있었다. 하지만, 이러한 관점의 실용적인 가치는 제한적이다? 이유 : 여러 데이터 집합들의 모임에 대한 평균을 바탕으로 했으므로, 만일, 실제 데이터인 관측 집한만이 주어지는 경우가 많은 경우 제약이 있음
- If we had a large number of independent training sets of a given size, we would be better off combining them into a single large training set which would reduce over-fitting
만약 특정 크기의 훈련 집합이 여러 개가 있다면, 하나의 큰 훈련 집합으로 합쳐서 사용하는 것이 더 효율적일 것.물론, 이렇게 하는 것이 주어진 모델 복잡도하에서 과적합의 정도를 줄이는 데도 도움
- Bayesian treatment may provide insights into the issues of over-fitting and lead to practical techniques for addressing the questions for model complexity.
이러한 한께점을 바탕으로 앞으로는 linear basis function model에 대한 베이지안 방법론을 살펴볼 것이다. 이는 과적합 문제에 대한 강력한 통찰과 모델 복잡도에 대한 질문을 해결하기 위한 실질적인 테크닉을 제공할 것이다.
'패턴인식과 머신러닝 > Ch 03. Linear Models for Regression' 카테고리의 다른 글
| [베이지안 딥러닝] Ch3.5 The Evidence Approximation (0) | 2021.02.18 |
|---|---|
| [베이지안 딥러닝] Ch3.3 Bayesian linear regression (0) | 2021.02.13 |
| [베이지안 딥러닝] Ch3.1 Linear models for Regression (MLE) (0) | 2021.01.18 |


댓글