2020-2학기 서강대 김경환 교수님 강의 내용 및 패턴인식 교재를 바탕으로 본 글을 작성하였습니다.
2.5 The Normal Density
Bayes 분류기의 구조는 사전 확률 $P(w_i)$뿐만 아니라, 조건부 밀도 $p(\mathbf{x}|w_i)$에 의해서 결정된다. 다양한 밀도 함수들이 존재하지만, multivariate normal 또는 gaussian density만큼 주목받은 것도 없다. 이유는 해석학적으로 다루기 쉽기 때문이다. (analytical tractability, 미분, 적분 등에 용이한, $e$로 구성됨)
그리고, 주어진 class $w_i$에 대한 특징 벡터 $\mathbf{x}$가 단일 대표 또는 프로토타입 벡터 $\mu_i$의 연속적 값을 갖고 랜덤하게 설정된 경우를 위한 적합한 모델이다. 이 절에서는 분류 문제들을 위한 최대 관심 대상 특성들에 초점을 맞추면서 다변량 정규 분포의 간단한 설명을 다룬다.
- Recall the definition of the expected value of a scalar function $f(x)$, defined expectation for some density $p(x)$:
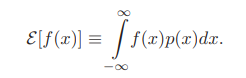
- If the values of the feature $x$ are restricated to points in a discrete set $D$.
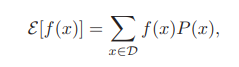
▶ Univariate Density
We begin with the continuous univariate normal or Gaussian density,

- mean ($\mu$)
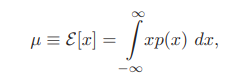
- Variance ($\sigma^2$)
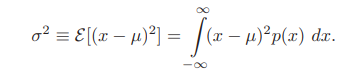
- $p(x) \sim N(\mu, \sigma^2)$ (즉, $x$가 평균 $\mu$와 분산 $\sigma^2$를 갖고 normal하게 분포)

▶ Multivariate Density
The general multivariate normal density in $d$ dimensions is written as
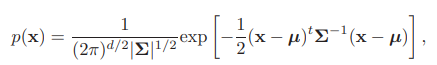

- mean vector

- covariance matrix
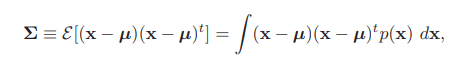
- statistical independence
예를 들어, 생선 모집단의 길이($x_i$)와 무게($x_j$) 특징들에 대해 양 공분산을 생각해보자. 만일, $x_i$와 $x_j$가 통계적으로 독립이면 $\sigma_{ij} = 0$이다. 만일 모든 비대각선 요소들이 0이면, $p(\mathbf{x})$는 $\mathbf{x}$의 요소들에 의해 univariate normal densities의 곱으로 축소된다. (?)
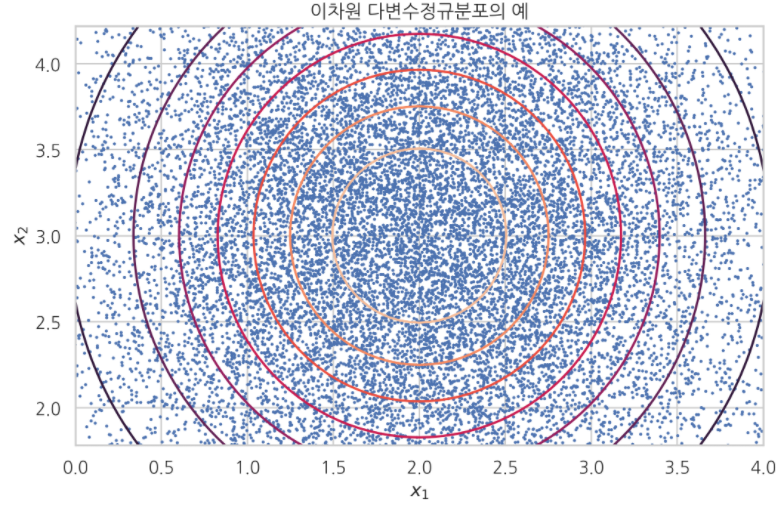
예제 1 : 두 변수가 독립인 경우 - 모수(parameter)가 다음과 같다고 하자.
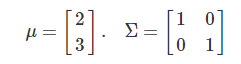
공분산 행렬로부터 $x_1$와 $x_2$가 독립이라는 것을 알 수 있다. 확률밀도함수를 구하면 다음과 같다.

위의 모수를 가진 sample을 뽑은 결과를 시각화시키면 다음과 같다.
예제 2 : 두 변수가 독립이 아닌 경우 - 모수(parameter)가 다음과 같다고 하자.
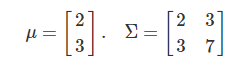
공분산 행렬로부터 $x_1$와 $x_2$가 양의 상관관계가 있다는 것을 알 수 있다. 확률밀도함수를 구하면 다음과 같다.
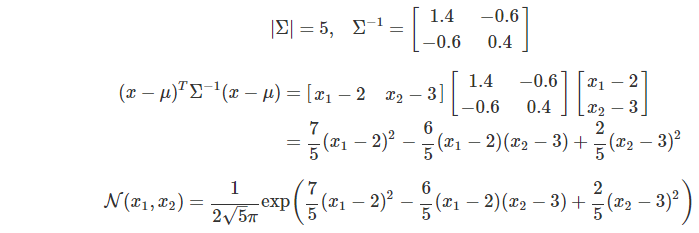
위의 모수를 가진 sample을 뽑은 결과를 시각화시키면 다음과 같다.

- Linear combination of jointly normally distributed random variables, independent or not, are distributed.
즉, 독립적이든 아니든, 결합적으로 normal하게 분포하는 랜덤 변수들의 선형 결합(Transformation)은 역시 normal하게 분포한다. 이를 수식적으로 표현하면 아래와 같다.

3가지 Case별로 선형 결합을 시킨 경우에 대한 각각의 시각화이다.

- Whitening transform (백색 변환)
때로는 임의의 mitivariate normal density를 구형(Spherical) 분포 - 즉, 공분한 행렬이 항등 행렬 $\mathbf{I}$에 비례하는 분포로 전환하는 linear transformation(좌표 변환)을 수행하는게 편리하다. (Figure 2.8에서의 ① 변환에 해당)


신호 처리에서 위 선형변환은 변환된 분포의 고유값들의 스펙트럼을 균일하게 만들기 때문에, 같은 의미로 백색 변환을 만든다고 한다.
예제 3 : 아래의 multivariate normal density를 whitening transform 시켜보자.

반드시 직접 풀어보자. eigenvalue 및 eigenvector 관한 설명은 4.1 Eigenvectors and Eigenvalues를 참고하도록 하자.


즉, 임의의 공분산 Matrix에 백색변환(선형변환 中 special case)를 하면 공분산을 항등행렬로 만들 수 있다. 이를 시각화한 결과는 다음과 같다.
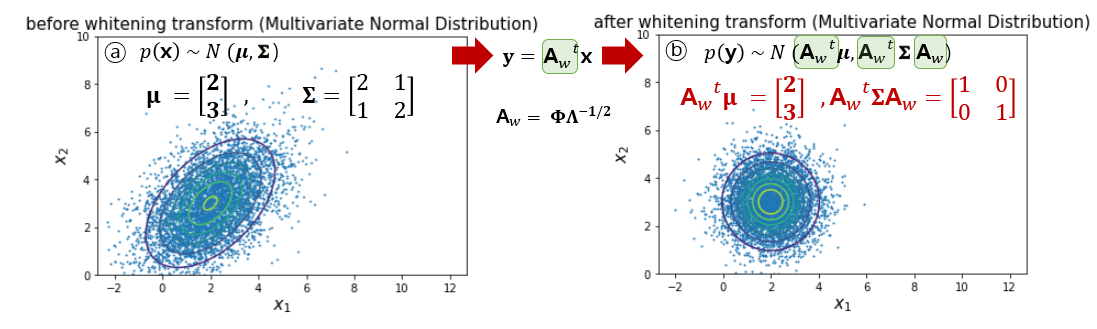
변환하기 전/후나 평균(mean)은 각각 [2, 3]으로 똑같지만, 공분산의 경우 [[2,1], [1,2]] (before) 에서 [[1,0], [0,1]]로 항등행렬로 변환되었음을 확인할 수 있다. (이런 경우 두 변수는 서로 독립이라고 말 할 수 있음). 즉 일반화하면 각 feature들 간의 관계(correlation)를 uncorrelation으로 만들어 줌
- $\Phi$ : Rotated
- $\Lambda^{-\frac{1}{2}}$ : scailing 작업
위 예제의 python으로 구현 결과는 아래 링크로 접속하여 참고하면 됩니다. Whitening transformation code
DeepHaeJoong/pattern_classification
패턴인식 연습문제 및 code 정리. Contribute to DeepHaeJoong/pattern_classification development by creating an account on GitHub.
github.com
- parameters 갯수 : $d+d(d+1)/2$ (직접 추론해보기)
- In the figure right :
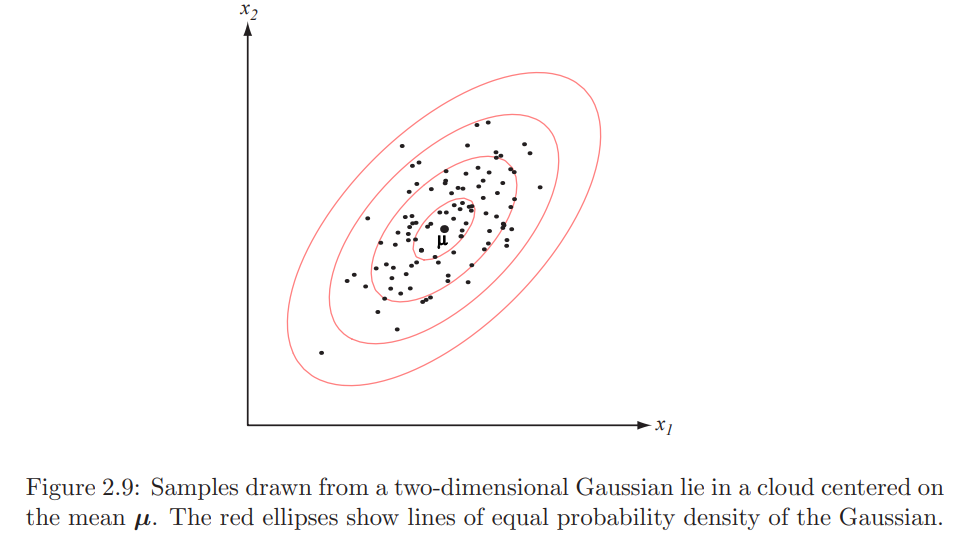
- Mahalanobis distance (from $\mathbf{x}$ to $\mu$) :

다음 Ch2.6에서는 "Discriminant Functions for the Normal Density" 를 다루도록 하겠습니다.
Reference




댓글