2020-2학기 서강대 김경환 교수님 강의 내용 및 패턴인식 교재를 바탕으로 본 글을 작성하였습니다.
2.1 Introduction
"Bayes decision theory"는 패턴 인식 문제에 대한 중요한 통계적(Statistical) 접근 방식임.
- This approach is based on quantifying the tradeoffs between various classification decisions using probability and the costs that accompany such decisions.
즉 , 확률을 이용하는 다양한 분류 판정들과 그러한 판정들에 수반하는 비용간의 절충을 정량화하는 것에 기반함
이 방식은 판정 문제가 확률론적 방식으로 표현되며, 모든 관련 확률 값들이 알려져 있다고 가정하지만, 이번 "Ch2"에서는 이론 관련하여 예제를 다루기 위해 확률론적 구조가 완전하게 알려져 있지 않을 때 일어나는 문제들임을 참고
In the example
컨베이어 벨트를 따라 도착하는 생선을 지켜보고 있는 관찰자는 다음에 어떤 종류가 올 것 인지 예측하는데 어려움을 겪고 있으며, 생선 종류의 시퀀스가 랜덤한 것처럼 보인다고 가정하자. 우리는 생선이 나타날 때 마다 state of nature( $w$)가 두 개 가능한 상태 중 하나라고 말할 것이다. (아래 참고)
- $w$ = $w_1$ : sea bass
- $w$ = $w_2$ : salmon
이처럼 $w$는 예측불허하기 때문에 이를 확률적으로 표현되어야 하는 확률 변수($w$)로서 고려하자.
만일, 잡힌 숫자가 "sea bass"와 "salmon"이 비슷하다면, 다음 생선이 "sea bass" 또는 "salmon"일 확률이 같다고 다음과 같이 표현할 수 있다.
$$P(w_1) = P(w_2)$$
보다 일반적으로, 다음 생선이 각각의 생선인 경우를 다음 아래와 같이 가정할 수 있다. 사전 확률(A priori probability, 또는 단순히 prior)가 있다고 가정하자.
A priori probability
이 사전 확률들은 실제로 생선을 관찰하기 전에 sea bass 또는 salmon을 잡게 될 확률이 얼마나 되는가에 대한 우리의 사전 지식을 반영함
- $P(w_1)$ : the next fish is sea bass
- $P(w_2)$ : the next fish is salmon
- $P(w_1) + P(w_2) = 1$ if no other types of fish (확률의 합은 항상 1을 만족해야함)
Decision Rule
볼 수 없는 상태에서 다음에 나타날 생선의 종류를 판단해야 한다고 잠시 가정해보자. 이처럼 정보가 없는 상태에서 판정해야 한다면, 아래 규칙을 이용해서 하는게 논리적일 것이다.
- $P(w_1) \gt P(w_2)$이면 $w_1$ 판정
- $P(w_1) \leq P(w_2)$이면 $w_2$ 판정
위와 같이 정보가 없는 상태에서 판정을 해야한다면, 판정에 수반하는 비용이 너무 클 것이다. 하지만, 현실에서는 적은 환경 정보만을 갖고 판정을 내리라고 요구되지 않는다. 분류기를 개선하기 위해 추가적으로 밝기 측량 $x$를 사용할 수 있다.
Class-conditional probability density function. (likelihood) $p(x|w)$ ← pdf이기 때문에 소문자로 표현
종류가 다른 생선은 다른 밝기 값으로 읽힐 것이고, 즉, 밝기의 변화 $x$를 해당 분포가 state of nature에 종속된 것을 확률적으로 표현하면 다음과 같다.
- $p(x|w_1)$ : $w_1$일 때 $x$라는 특징(밝기)을 가질 확률 분포
- $p(x|w_2)$ : $w_2$일 때 $x$라는 특징(밝기)을 가질 확률 분포
아래 그림은 $p(x|w_1)$과 $p(x|w_2)$ 간의 차이는 sea bass와 salmon 모집단 간의 밝기의 차이를 묘사한다.

패턴이 부류 $w_1$에 속한다고 할 때 특정 특징 값 $x$를 측정할 확률 밀도를 보여주는 가설적 조건부 클래스-확률 밀도 함수, 만일 $x$가 생선의 밝기를 나타낸다면, 두 곡선은 두 종류의 생선의 모집단과 밝기 차이를 묘사함. 밀도 함수들은 정규화되며, 따라서 각 곡선의 밑의 면적은 1.0 이다.
|
Q) 어떻게 $p(x|w_1)$ 및 $p(x|w_2)$를 얻을 수 있을까? 고민해보자. |
A) 어부가 sample로 부터 얻은 것 (학습 관점에서 얻음)
Joint probability density (결합 확률 분포)
- $p(w_j, x) = p(x, w_j) $ (확률의 대칭성)
- $P(w_j|x)p(x) = p(x|w_j)P(w_j)$ (확률의 곱의 법칙)
- $P(w_j|x) = \frac{p(x|w_j)P(w)}{p(x)}$ (베이즈 공식)
위 두 성질을 이용하여 Bayes formula를 추론할 수 있으며, 자세한 설명은 아래의 해당 자료를 참고하면 된다.
2020/07/09 - [패턴인식과 머신러닝/Ch 01. Introduction] - 1.2 Probability Theory
Bayes formula (베이즈 공식)
$$P(w_j|x) = \frac{p(x|w_j)P(w)}{p(x)}$$
여기서는 "bass sea" 및 "salmon" 문제의 경우
$$p(x)=\sum_{j=1}^{2} p\left(x \mid \omega_{j}\right) P\left(\omega_{j}\right)$$
이다. 이는, 분류를 결정하는 요소는 아니지만, 이게 들어감으로써 posterior 분포를 0 ~ 1 인 확률값으로 정규화 역할
Bayes 공식을 말로는 다음과 같이 표현할 수 있음
$$\text {posterior}=\frac{\text {likelihood} \times \text {prior}}{\text {evidence}}$$
Bayes 공식은 $x$의 값을 관찰함으로써 사전 확률 $P(w_j)$를 사후 확률 $P(w_j|x)$ - 특정값 $x$가 측정되었다고 했을 때 state of nature가 $w_j$일 확률 - 로 전환할 수 있다.
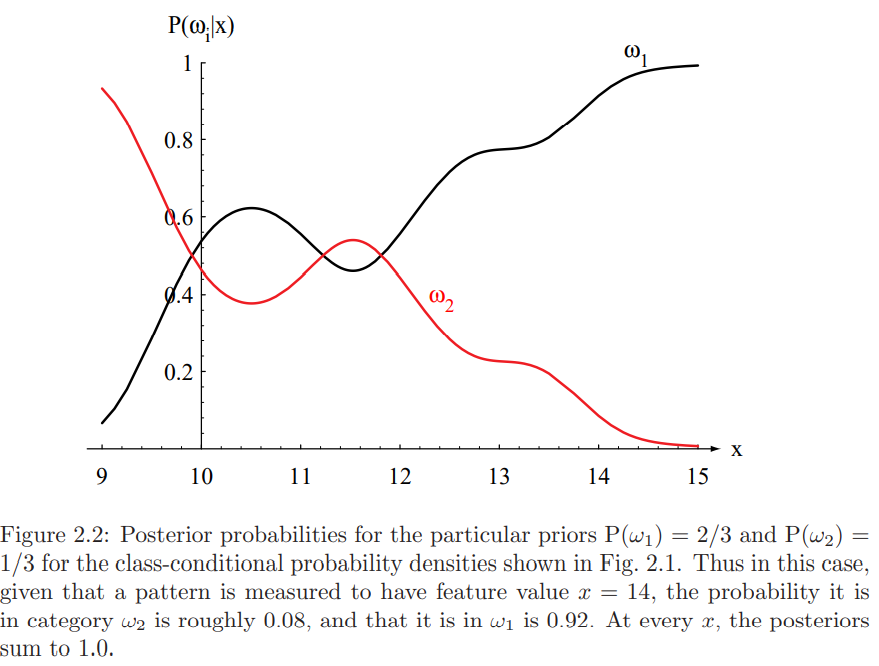
아래 그림은 $P(w_1) = 2/3$ 및 $P(w_2) = 1/3$ 일 때, 사후 확률 분포를 보여준다.
 |
Figure 1는 Class-conditional probability density function이며, Figure 2는 Posterior probabailites를 나타내고 있다. Bayes Formula의 효과는 prior 정보로 인해서 결과 밝기가 $x=11$이라는 지점서의 $w2$ 및 $w_1$에 속할 의사 결정 확률이 달라지는 것을 보여준다.
만일 $P(w_1|x)$가 $P(w_2|x)$보다 큰 관찰 $x$가 있다고 하면, 당연히 state of nature로써 $w_1$이라고 판정을 내릴 것이다. $P(w_2|x)$가 $P(w_1|x)$보다 큰 관찰 $x$가 있다고 하면, $w_2$를 선택할 것이다.
$$\text { Decide } \omega_{1} \text { if } P\left(\omega_{1} \mid x\right)>P\left(\omega_{2} \mid x\right) ; \quad \text { otherwise decide } \omega_{2}$$
이 판정 절차를 증명하기 위해 우리가 판정을 내릴 때마다 에러의 확률을 계산하자. 어떤 특징 $x$를 관찰할 때마다 에러의 확률은
$$P(\text {error} \mid x)=\left\{\begin{array}{ll}
P\left(\omega_{1} \mid x\right) & \text { if we decide } \omega_{2} \\
P\left(\omega_{2} \mid x\right) & \text { if we decide } \omega_{1}
\end{array}\right.$$
이다.
분명히, 주어진 $x$에 대해 $P(w_1|x) \gt P(w_2|x)$이면 $w_1$, 그렇지 않으면 $w_2$로 판정함으로써 에러의 확률을 최소화할 수 있다. 물론 똑같은 $x$의 값을 두 번 관찰하지 못할 수 있다. 이 룰이 에러의 평균 확률을 최소화할 것인가? 그렇다. 왜냐하면, 에러의 평균 확률은
$$P(\text {error})=\int_{-\infty}^{\infty} P(\text {error,}, x) d x=\int_{-\infty}^{\infty} P(\text {error} \mid x) p(x) d x$$
으로 주어지며, 만일 모든 $x$에 대해서 $P(\text {error} | x)$를 가능한 한 작게 만든다면, 이 적분은 가능한 한 작아야 하기 때문이다. 따라서 에러 확률을 최소화하기 위한 다음의 Bayese 판정 룰의 정당성을 증명했다.
$$\text { Decide } \omega_{1} \text { if } P\left(\omega_{1} \mid x\right)>P\left(\omega_{2} \mid x\right) ; \quad \text { otherwise decide } \omega_{2}$$
이 룰 하에 의해서 다음과 같이 정리된다.
$$P(\text {error} \mid x)=\min \left[P\left(\omega_{1} \mid x\right), P\left(\omega_{2} \mid x\right)\right]$$
즉, 사후 확률을 더 강조
$$\text { Decide } \omega_{1} \text { if } p\left(x \mid \omega_{1}\right) P\left(\omega_{1}\right)>p\left(x \mid \omega_{2}\right) P\left(\omega_{2}\right) ; \quad \text { otherwise decide } \omega_{2}$$
보다 특수한 경우를 고려하면 다음과 같이 간단히 이해할 수 있다.
- If $p(x|w_1) = p(x|w_2)$ : the decision is based on the prior probabilities
- If $P(w_1) = P(w_2)$ : the decision is based on $p(x|w_j)$
하지만, 실제 현상에서 "Prior"가 주어질까? 답은 : 주어지지 않는게 대부분이다. 따라서, "Prior"를 균등하게 봐야하며, 사후 확률에 영향을 미치는 요소는 likelihood 이다.
다음 Ch2.2 에서는 "Bayes decision theory - continious features" 를 다루도록 하겠습니다.
Reference




댓글