이 글은 Edwith로 부터 제공되는 주재걸 교수님의 "인공지능을 위한 선형대수" 강의를 듣고 요약하였으며, 개인 공부를 위해 부족한 부분을 위해 필요한 개념들을 추가하여 작성하였습니다.
이번 절(3.4)에서는 "그람-슈미트 직교화(Gram-Schmidt Orthogonalization)", "OrthonormalQR분해(QR Factorization)"의 정의 및 개념을 알아보고, 예제를 직접 풀어면서 이해를 돕고자 한다.
이번에는 임의의 행렬을 직교기저(Orthogonal basis)를 가지는 행렬로 변환하는 그람-슈미트 직교화에 대해 배워보겠습니다.
Gram-Schmidt Orthogonalization
Gram-Schmidt Process의 Idea는 다음과 같다.
먼저, Basis가 2개의 Vector로 이루어진 경우를 보자.

다음, Basis가 3개의 Vector로 이루어진 경우를 보자.

위의 과정을 보면 모두 동일하고, 다만 Matrix의 dim에 따라서 같은 프로세스가 추가된다. 이를 일반화 시키면 다음과 같다.

Orthogonal basis를 다 구하고나서 계산 및 편의를 위해 Vector들에 Scale을 해도 상관 없다. (옵션)
Step n+1 : (optional). If appropriate, scale 𝐯2 to simplify later computations, e.g.,

QR Factorization
QR Factorization of Matrices 는 선형 독립인 Column들로 구성된 Matrix A (m x n)를 Gram-Schmidt 도구를 활용하여 다음 Step에 Q Matrix와 R Matrix로 분해된다.
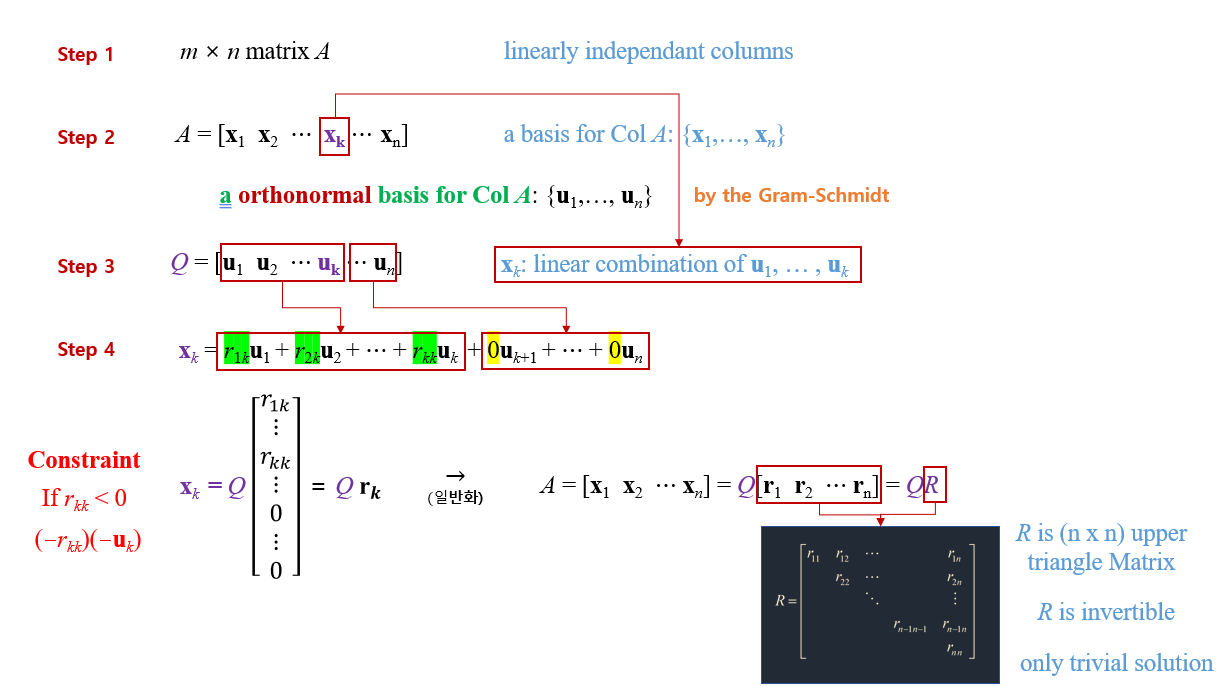
참고 : R Matrix의 digonal 값이 항상 양수로 만들어 줘야한다. (제약 조건 걸어둠)
QR Factorization 정리하면 다음과 같다.


Example: QR Factorization
반드시 직접 풀어보기!!



반드시, 눈으로만 보지 말고 직접 풀어보면서 앞에서 배운 정리를 이용하여 전개 필요!
'Linear Algebra (선형대수학) > Ch 3. Least Square' 카테고리의 다른 글
| 3.3 Orthogonal Projection Ⅰ& II (0) | 2019.11.23 |
|---|---|
| 3.2 Normal Equation (0) | 2019.11.23 |


댓글